Simone Fiorentini MSc Publications

Biography Simone Fiorentini was born 1992 in Verona, Italy. He received his Bachelor degree and Master Degree in Physiscs from the University of Padova, in 2014 and 2017, respectively. He carried out his Master Thesis at the Ruprecht-Karls University of Heidelberg through the Erasmus Program. After a short period working for an IT company in Milan, Italy, he joined the Institute for Microelectronics in November 2018, where he started his PhD studies. He is currently investigating ways to appropriately simulate both spin and magnetization dynamics in non-volatile magnetic memory devices.

Emerging non-volatile spin-transfer torque (STT) magnetoresistive random access memories (MRAM) offer high speed and endurance, and are attractive for stand-alone, embedded automotive, MCU, and IoT applications, as well as frame buffer memory and slow SRAM. The core of an MRAM cell is the Magnetic Tunnel Junction (MTJ) consisting of a CoFeB reference layer (RL) and a free magnetic layer (FL), separated by an MgO tunnel barrier (TB). The use of MTJs with perpendicular magnetic anisotropy (PMA), provided by the interface with the MgO tunneling layer, allows the achievement of higher TMR values. In order to boost the PMA, the FL is often interfaced with a second MgO layer. Recently, more advanced structures were proposed to boost the PMA even further, either by introducing more MgO layers in the FL, or by using the shape anisotropy of elongated FLs while also improving scalability, thanks to a reduced diameter. In order to model such devices, it is paramount to generalize the traditional Slonczewski approach for the torque computation (applicable only to thin FLs) to incorporate normal metal buffers or MgO barriers between multiple CoFeB free layers, as well as the barrier between the RL and FL, and the torques coming from magnetization textures or domain walls that can be generated in elongated FLs. For this purpose, we developed an extension of the drift-diffusion formalism for the computation of the torque to the presence of MTJs in the structure.

To evaluate the charge current density, we model the TB as a poor conductor with a local resistance dependent on the relative orientation of the magnetization across the TB. The density can then be used to compute the spin accumulation and extract the torque acting on the magnetization. To correctly model the spin current density, the coupled spin and charge drift-diffusion approach must be supplemented by appropriate boundary conditions for the spin current at the TB interfaces. With the addition of such conditions, the expected dependence of the torques on the relative angle between the magnetization vectors is reproduced (Fig. 1). Our approach can be generalized to model non-linear bias dependences of the torques as an on-demand feature by making the interface polarization parameters depend on the voltage. The observed voltage dependencies of both the damping-like and field-like torques are thereby properly reproduced (Fig. 2). The magnetization in elongated FLs of ultra-scaled MRAM cells during switching is highly non-uniform along the FL as the formation and propagation of a domain wall is expected. The additional torques acting in the presence of a domain wall are usually modeled by the Zhang and Li expression. We demonstrate that, in the presence of a TB, the Slonczewski and Zhang and Li torques are not additive, and must be treated on equal footing to correctly describe the torques acting on non-uniform magnetization in elongated FLs with several MgO TBs (Fig. 3).

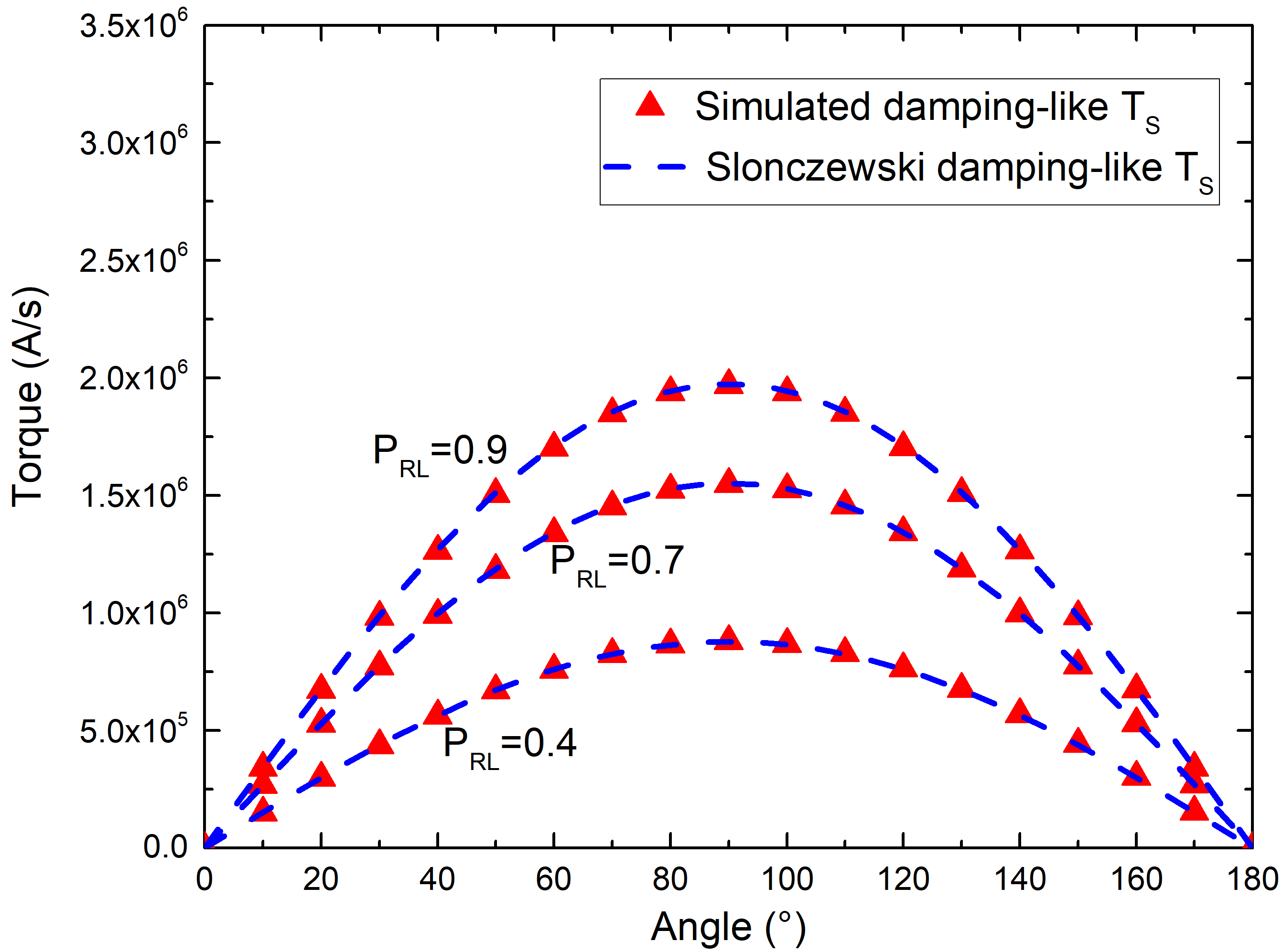
Fig. 1: Angular dependence of the torque with the spin-current boundary conditions, for semi-infinite FL and RL. The expected sinusoidal angular of an MTJ is reproduced, for several values of the RL spin polarization parameter.

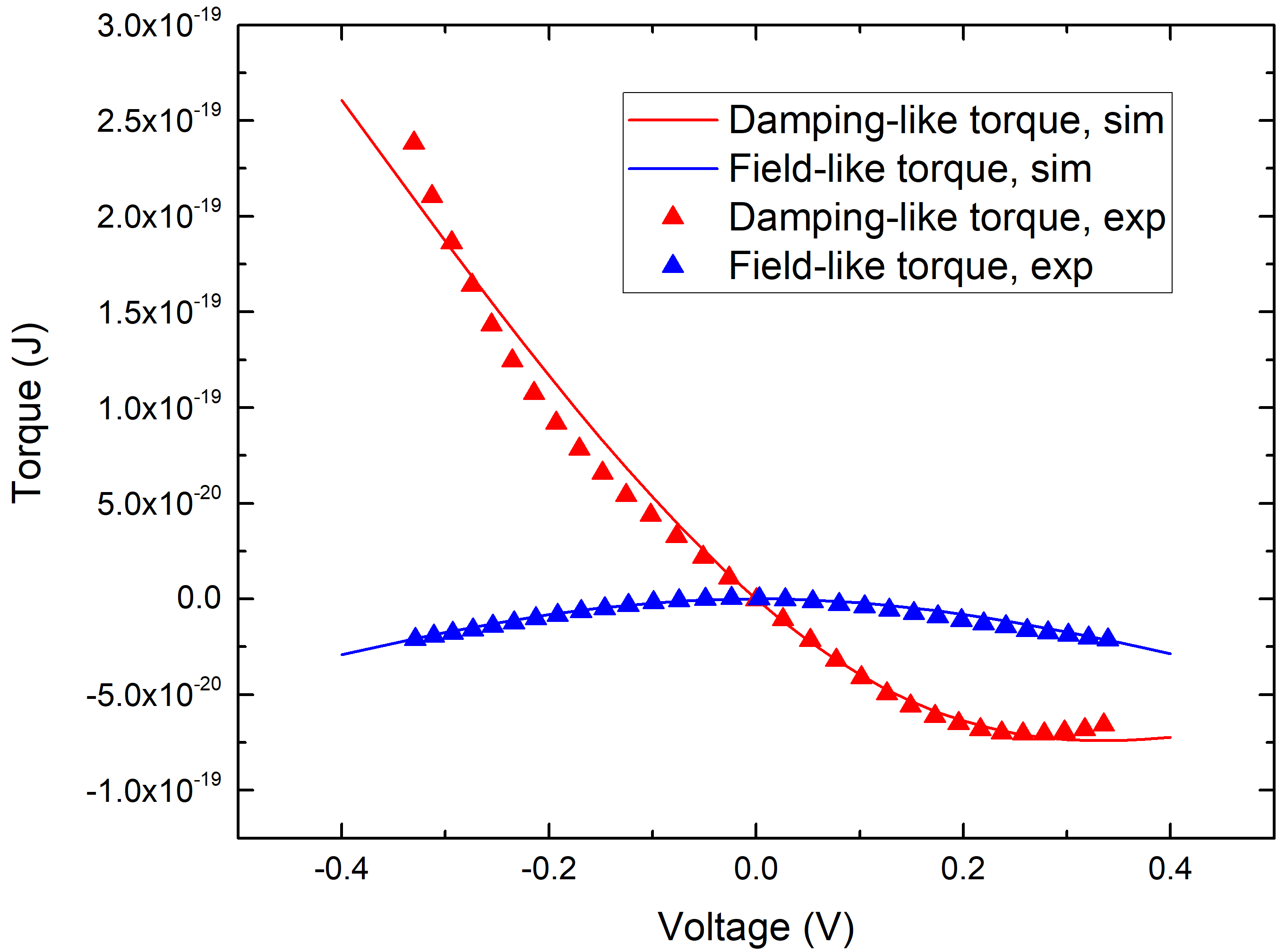
Fig. 2: Dependence of the torques on the bias voltage, compared with experimental results.

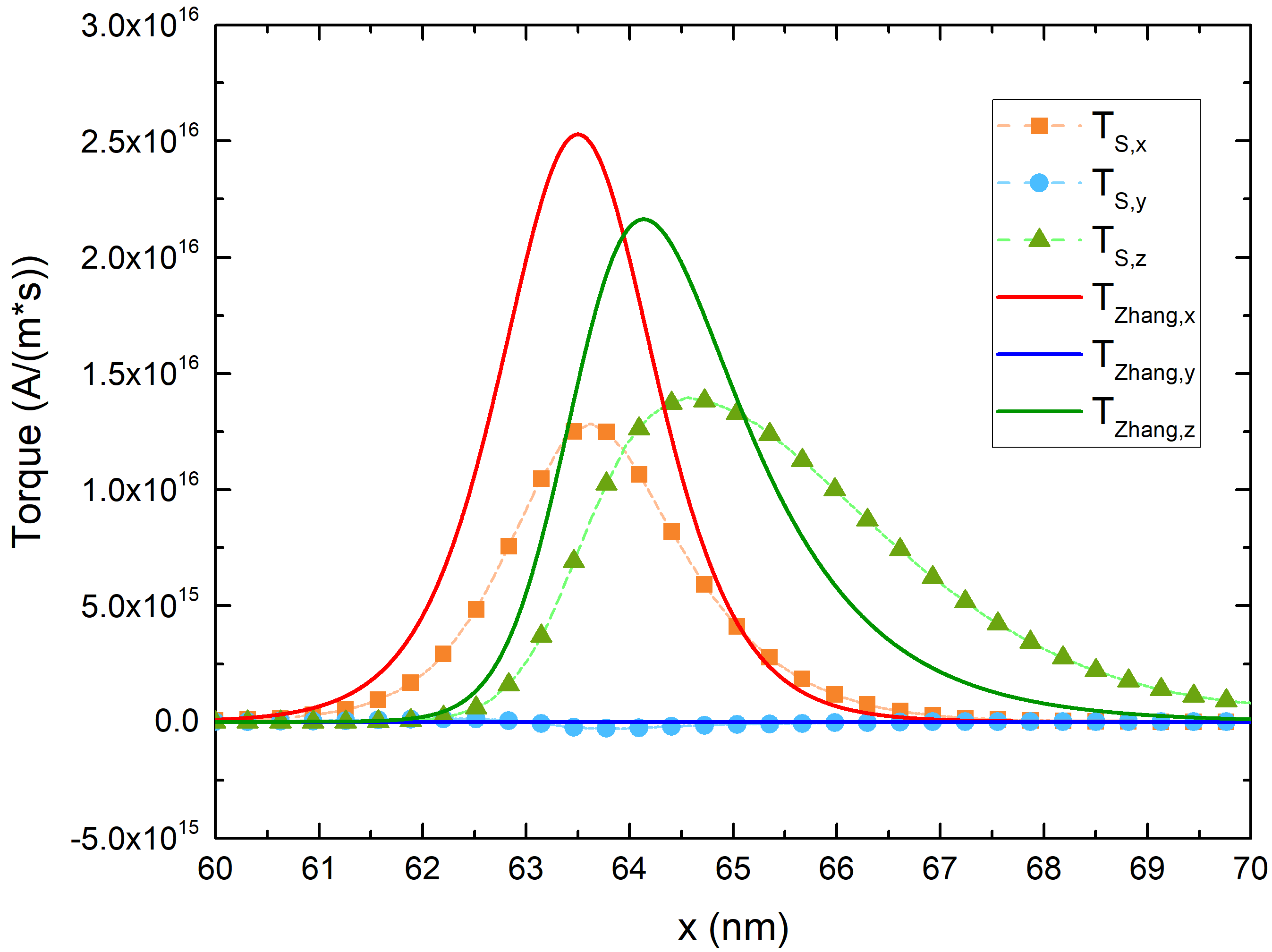
Fig. 3: Close-up of the bulk spin torque T_S compared to the Zhang-Li torque T_Zhang acting on the FL of an MRAM cell with elongated ferromagnetic layers. The magnetization in the RL points in the x direction, while in the FL the magnetization rotates from the z to the -x direction across the layer. The presence of the MTJ influences also the bulk portion of the torque, caused by the magnetization gradient, making the unified approach the most suitable for dealing with ultra-scaled MTJs with elongated ferromagnetic layers.