Paul Manstetten Univ.Ass. Dipl.-Ing.(FH) Dr.techn. MSc Publications

Biography Paul Manstetten was born in 1984 in Berlin, Germany. He studied Mechatronics at the University of Applied Sciences Regensburg (Dipl.-Ing.) and Computational Engineering at the University of Erlangen-Nuremberg (MSc). After three years as an application engineer for optical simulations at OSRAM Opto Semiconductors in Regensburg he joined the Institute for Microelectronics in 2015 as a project assistant. He finished his PhD studies (Dr.techn.) in 2018 and works as a postdoctoral researcher on high performance methods for semiconductor process simulation.

The Nudged Elastic Band (NEB) method and its variants are a common choice used to identify potential energy surface (PES) saddle points between two given atomic configurations of a system of interest. Density functional theory (DFT) is a popular and versatile choice to evaluate the PES numerically. Due to the high computational demands of DFT calculations, active research to reduce the total number of required evaluations when approximating energy barriers with NEB calculations is ongoing. We investigate an approach wherein a surrogate model based on Gaussian process regression (GPR) is constructed during a NEB calculation in order to replace a portion of the computationally expensive DFT calculations.

An important prerequisite for a GPR model is the selection of a covariance function to model differences between each possible pair of observations. Typically, a GPR implementation provides a set of commonly used application-agnostic covariance functions. Using a domain-specific covariance function can have one or more of the following desired effects: (a) control over the number of hyperparameters (b) possibility of physically motivated interpretation of hyperparameters (c) reduced variance in the predictions

If the observations used to train a GPR model contain derivative information (as is the case for DFT calculations which provide energies and forces for atomic configurations), higher-order partial derivatives of the covariance function are required. Relying on a composition of covariance functions further increases the complexity of the required terms. The effort for a manual implementation using a computationally efficient style (vectorization) can easily become huge, and the maintainability of the resulting source code is not ideal. Additionally, a straightforward extension to other covariance functions is, in general, not possible.

In order to advance the exploration of different covariance functions, is it important to reduce the implementation overhead until a covariance function can be applied and tested for an application. Automatic differentiation (AD) combined with auto vectorization (AV) is a promising approach to enable straightforward extensibility of a GPR framework with new covariance functions. The JAX package available for Python provides AD and AV capabilities combined with a dynamic pre-compilation based on large portions of the NumPy API. We are currently using JAX to reimplement selected covariance functions used in our GPR implementation to accelerate NEB calculations.

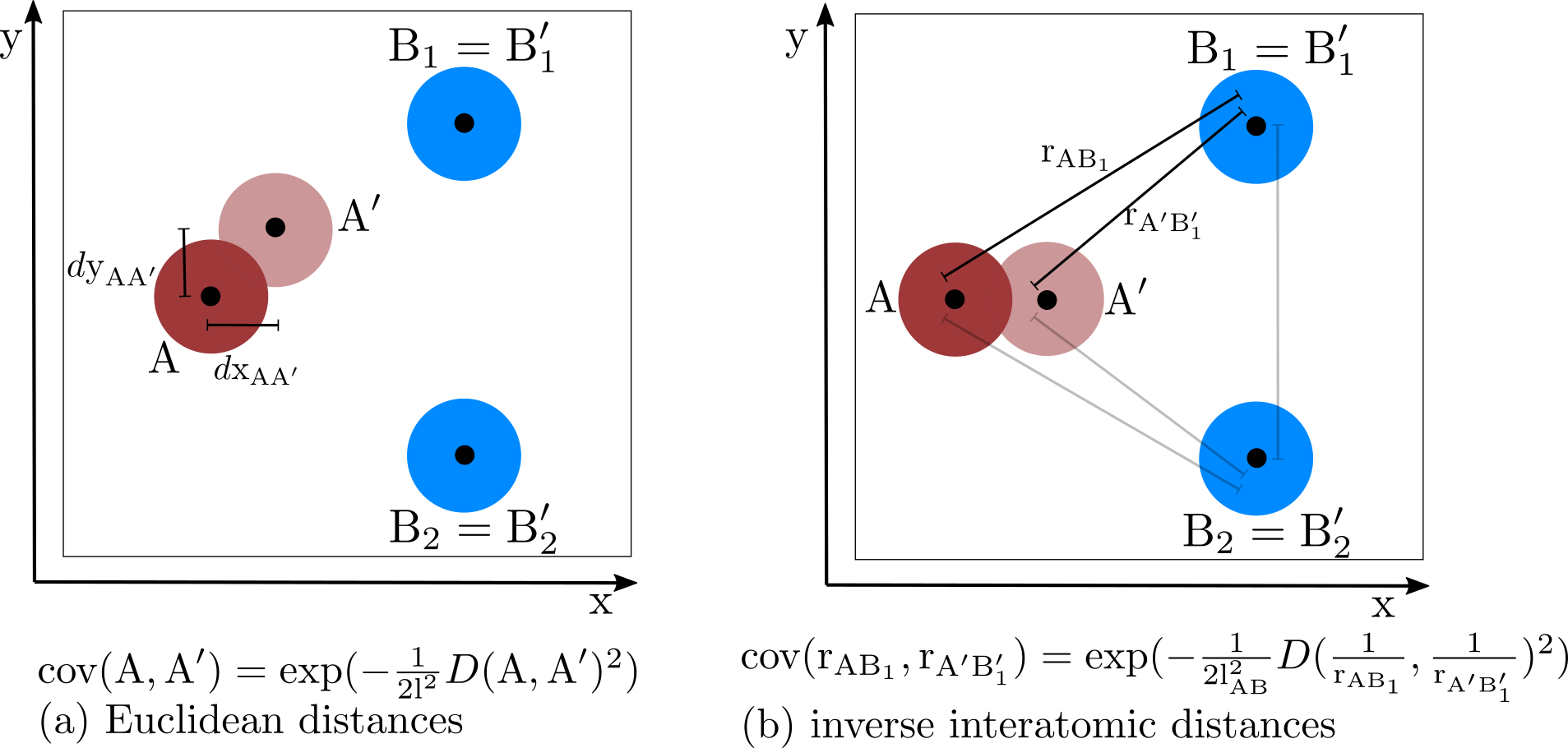
Fig. 1: Different covariance functions based on a squared exponential illustrated for an atomic configuration consisting of three atoms: (a) Using the Euclidean distance between atomic coordinates as difference measure and a single global length scale hyperparameter. (b) Using pairwise inverse interatomic distances as difference measure and a separate length scale hyperparameter for each group of atomic pair types.