Luiz Aguinsky MSc Publications

One demanding aspect of semiconductor processing is the fabrication of high aspect ratio (AR) structures. Examples of such structures are channel holes in three-dimensional (3D) negative-AND flash memory and through-silicon vias. A key challenge in high AR fabrication is the insufficient supply of neutral reactants towards the bottom of a feature. In deposition scenarios, this phenomenon manifests as a sharp decline in step coverage with higher ARs, whereas in plasma etching, it is linked to AR-dependent etching.

The fundamental physical characteristic of neutral transport is the presence of diffuse reflections. This leads to the conventional approach to studying neutral fluxes in high AR structures: Solving the radiosity equation, which describes the net exchanges between all surfaces. This can be accomplished either by randomly sampling particle transport, with Monte Carlo ray tracing, or by explicitly discretizing the surfaces and inverting the exchange matrix. In cases where the sticking probability is low, however, these methods can struggle to compute the fluxes. Monte Carlo methods then require a very large number of rays, and the matrix resulting from explicit discretization becomes ill-conditioned.

Since low sticking probability cases are common, particularly in deposition processes, a more robust method is necessary. One common approach is Knudsen diffusion: A preferred direction of transport is established, and a one-dimensional diffusion-type equation is derived from physically motivated approximations to the cross-sectional mass balance. We propose an extension to the standard Knudsen diffusion approach by including two additional terms in the mass balance: A geometric factor and the direct flux from a source. The geometric factor extends the approach beyond the standard infinite cylinder approximation, enabling a more accurate description of the indirect flux due to reflections. The direct flux is introduced to recapture the correct flux towards the bottom, which can be underestimated in the standard Knudsen approach.

A schematic representation of the mass balance is shown in Fig. 1. This results in a system of coupled ordinary differential equations, represented in Fig. 2, which makes the differences with respect to standard Knudsen diffusion explicit. In Fig. 3, we compare the extended Knudsen approach to both our reference discretized radiosity model and standard Knudsen diffusion for the case of a finite cylinder of AR 50 and a sticking probability of 1%. In summary, our extended Knudsen diffusion approach offers an alternative to conventional radiosity models, particularly for the challenging low sticking regime.

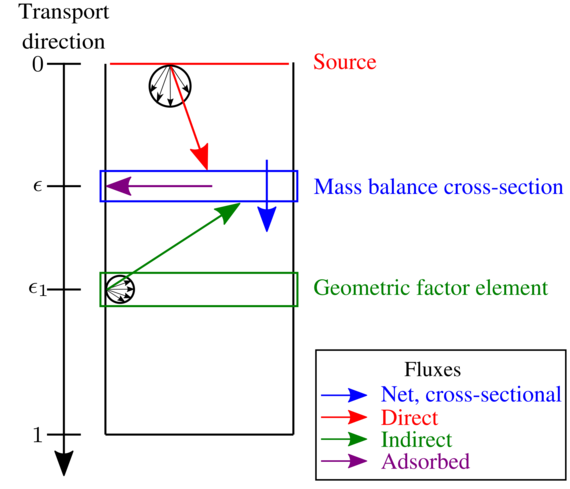
Fig. 1: Schematic representation of the model. The goal is to obtain the net, cross-sectional flux through the mass balance volume (blue) by balancing the direct (red), adsorbed (purple) and indirect (green) fluxes. The complete indirect flux contribution is obtained by integrating over all green elements.

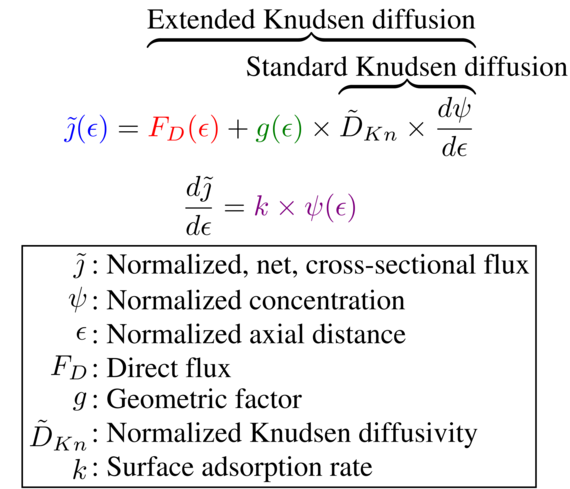
Fig. 2: Schematic representation of the resulting system of ordinary differential equations modeling neutral transport. The colors relate to Fig.1. We note the differences between our model and the standard Knudsen diffusion approach: The presence of direct flux and the geometric factor. The adsorbed flux is modeled by a volumetric sink term.

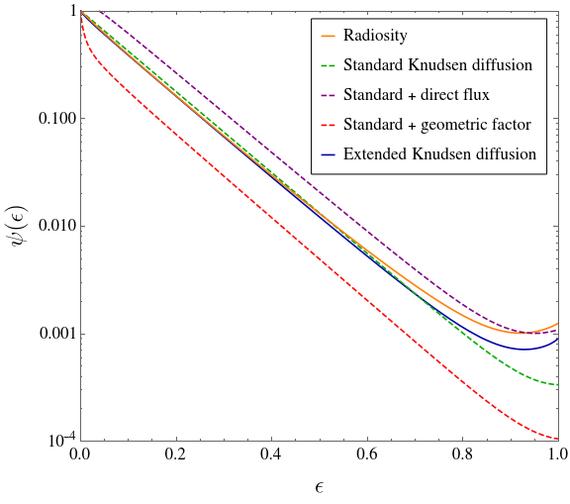
Fig. 3: Comparison of the local concentration between different approaches for a cylinder of AR 50 and a sticking probability of 1%. We note that the full extended Knudsen diffusion approach is required for more accurately matching radiosity over most of the feature.