 |
|
Biography
Majid Benam was born in Dehdasht, a small city in Iran, in 1988. He studied electrical engineering at Amirkabir University of Technology (AUT). He was then accepted to study his Master’s in Semiconductor Devices at Sharif University of Technology (SUT). After working for several International companies like Agfa HealthCare and Huawei Co., he joined the Institute for Microelectronics at TU Wien as a PhD student in 2017. His research interests include: Quantum Transport, Modeling of Semiconductor Devices, and Interconnects.
Self-Consistent Monte Carlo Solutions of the Wigner and Poisson Equations Using a Multigrid Approach
Although some level of understanding can be achieved by considering independent carriers while analyzing nanoscale transport, a more accurate description requires the use of self-consistent models, where carrier-carrier interactions are also taken into account. The self-consistent solver implemented in ViennaWD has two main components: A Wigner solver, which treats the Wigner potential as a generating mechanism and is responsible for the generation and annihilation of signed particles, and a Poisson solver, which uses an efficient multigrid approach to take the charge density distribution and update the value of the potential after each time step. The solver provides for the possibility of calculating physical quantities, such as carrier density and current. Initial and boundary conditions are carefully analyzed so that a consistent and compatible set is used in order to obtain accurate and reliable results. There is also the option to select a position-dependent relative permittivity in the Poisson equation, which enables the simulation of devices consisting of materials with different properties.
As illustrated in Fig. 1, the Monte Carlo simulation starts with an initialization step in which geometrical aspects and physical quantities, such as density and potential, are fed into the simulator via input files or internal functions. Some other simulation parameters and the boundary conditions are set and the properties of the particles to be injected into the region are also decided. The Wigner potential is then calculated, which in turn determines the statistics of the generation mechanisms. The Poisson solver is called in at each time step, using the current value of the charge density, and updates the value of the potential for the next time step. A charge redistribution scheme is then used to map charges among the neighboring cells in a more efficient way for the next iteration. The Monte Carlo evolution of particles is then performed using the Signed Particle Monte Carlo approach.
The Poisson step receives the updated value of the carrier density at each time step and utilizes a multigrid approach to provide the updated value of the electrostatic potential, which is then used to calculate the new Wigner potential, and hence the new statistics for the generation of new pairs of particles. The multigrid algorithm replaces the problem, which is on an initial fine grid as shown in Fig. 2, by an approximation on a coarser grid and uses the corresponding solution as a starting guess for the problem on the fine grid, which is then iteratively updated. Comparing the carrier density, when the Poisson equation is solved (Fig. 3; right) and when it is not solved (Fig. 3; left), shows the expected repulsion of the injected wavepackets (representing particles) in the former case.
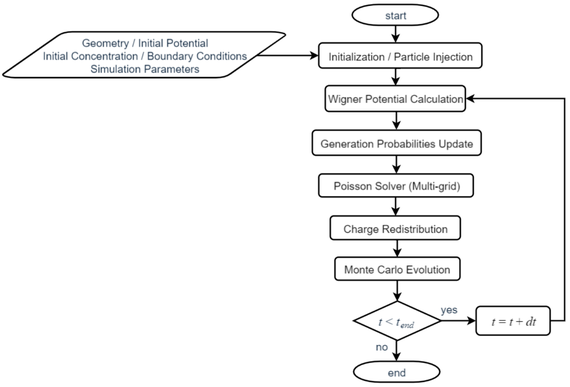
Fig. 1: Flowchart for the self-consistent solution of the Poisson and Wigner equations.
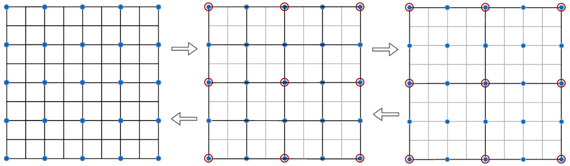
Fig. 2: Multigrid fine-to-coarse relaxation (left to right) and coarse-to-fine prolongation (right to left) schemes.
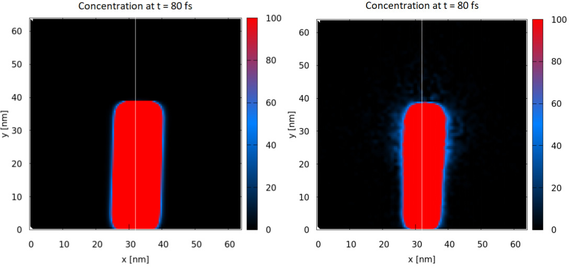
Fig. 3: Carrier density at t = 80 fs for cases in which the Poisson equation has been solved (right) and without the Poisson equation (left).



