 |
|
Biography
Johann Cervenka was born in Schwarzach, Austria, in 1968. He studied electrical engineering at the Technische Universität Wien, where he received the degree of Diplomingenieur in 1999. He then joined the Institute for Microelectronics at the Technische Universität Wien and received his PhD in 2004. His scientific interests include three-dimensional mesh generation, as well as algorithms and data structures in computational geometry.
A Deterministic Wigner Approach for Superposed States
The Wigner formalism is a convenient way of describing quantum mechanical effects through a framework of distribution functions in phase space. Currently, there are both stochastic and deterministic approaches in use. In our deterministic method, the critical discretization of the diffusion term is done through the utilization of an integral formulation of the Wigner equation. This deterministic method was studied in the context of superposed quantum states as a precursor to simulations of entangled states. In order to ensure its application to superposed wave packages, however, it is crucial that the correlation state be adequately handled.
Fig. 1 shows a surface plot of the Wigner function of two Gaussian wave packages with superposed wave functions. The packages move with the same speed to the right and pass a reflecting barrier. In phase space, the Wigner function consists of two Gaussian packages at the left and right, emanating from each wave package, plus an additional correlation state in between. The correlation state shows the same envelope and speed as the separate packages. Furthermore, it displays oscillatory behavior in k-space with a frequency that increases with the distance traveled by the packages. In contrast to classical distribution functions, the Wigner function may also produce negative values.
In Fig. 2, a time-shifted simulation when the right package reaches the barrier is shown. Even though only the right package reaches the barrier, the correlation state already feels the barrier and becomes affected. This information is located in the oscillation in k-space. Continuing in time, all three packages are reflected and propagate in the opposite direction. Although strict limits on the resolution in k-space have to be satisfied to properly resolve the oscillations, the coherence length in the calculation of the Wigner function consequently has to spawn at least the entire package group. These bounds may represent a challenge for the solution, which has to be analyzed in further work.
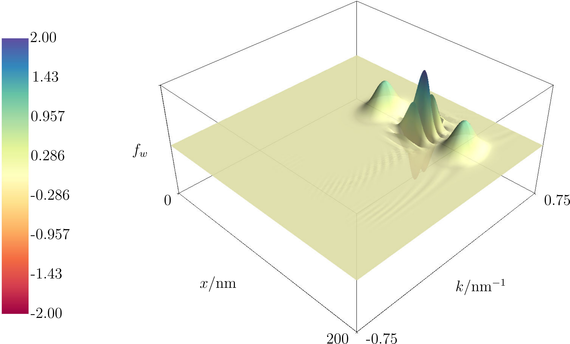
Fig. 1: The Wigner function of two Gaussian wave packages with superposed wave functions. The Wigner function consists of two Gaussian packages at the left and right, plus an additional correlation state in between.
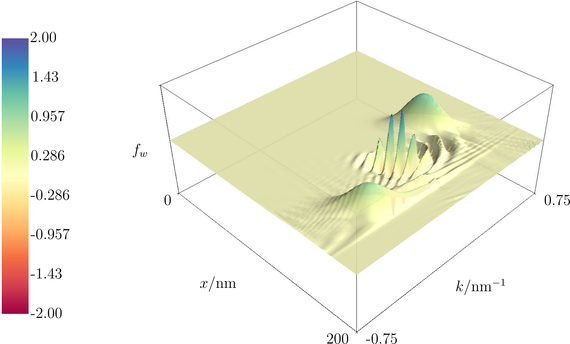
Fig. 2: Even though only the right package reaches the barrier, the correlation state already feels the barrier.



