Georgios Diamantopoulos MSc Publications

Simulation of an evolving interface is a problem that often arises during TCAD simulation. Typically, a level-set method is used in order to compute the evolution of the surface. Such methods do not enforce the signed distance field property, however, which is usually lost after an advection step. In order to restore this property, a process called re-distancing is used, for which a widely used method is the Fast Marching Method (FMM). This method is preferred in micro-electronics simulations because of its high accuracy compared with its alternatives. Due to the nature of the problems faced during TCAD simulation, high accuracy is demanded of the solution. In order to achieve this, the base (coarse) mesh is refined locally and finer meshes are defined around fine structures of the interface, such as sharp corners. This creates a hierarchy of meshes, with a coarse base mesh and finer meshes, which are generated after a refinement step at every level. In order to solve the re-distancing problem across the entire hierarchy, the solution on the base mesh is first computed, and then the solution is interpolated on the boundary of the finer meshes. The interpolated values, along with the zero level-set function on the interface, are used as the initial condition for the computation of the sign distance field on the finer meshes. The same procedure continues to the next level of finer meshes until the level with the finest resolution is computed.

The above-mentioned hierarchical mesh structure offers an inherent parallelization due to the multiple levels of increasingly fine meshes. Our approach provides a parallel FMM on a hierarchical mesh structure, where OpenMP tasks are used in order to compute the solution for each mesh independently. A synchronized data exchange approach is used for inter-mesh communication, effectively resolving dependencies among neighboring meshes. The algorithm is implemented in C++ with OpenMP parallelization, and the parallel performance is assessed on a dual-socket Ivy Bridge-EP compute node. Our benchmarks show that the method provides a high parallel efficiency in cases where the number of meshes is much higher (at least 10 times) than the number of threads.

Fig. 1 shows an example from a FinFET process flow. The coarsest (base) level contains one mesh with 84 x 72 x 312 cells, in the second (finer) level there are 100 meshes and there are four times more cells in each direction as compared to the coarsest mesh. Fig. 2 shows the parallel speed-up for a full-band re-distancing benchmark for the problem in Fig. 1. The parallel efficiency for the second level is high (approximately 88% for 8 threads) but is reduced after 8 threads when the second socket is introduced. The overall parallel efficiency is restricted due to the serial algorithm on the base level.

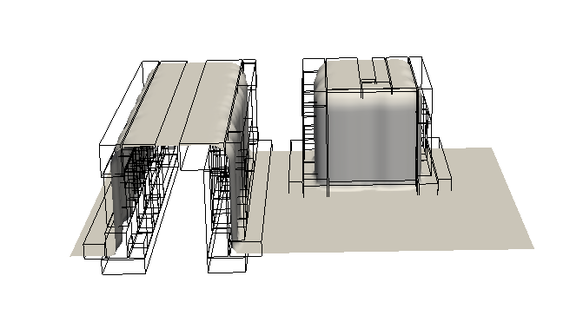
Fig. 1: Level 2 of a FinFET process flow simulation with 100 meshes.

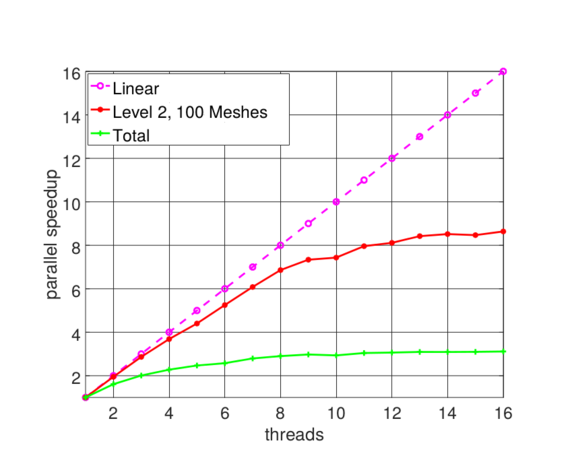
Fig. 2: Parallel speed-up for level 2, and the total computation of the problem (cf. Fig. 1).