 |
|
Biography
Hans Kosina received the Diplomingenieur degree in electrical engineering and PhD from the Technische Universität Wien in 1987 and 1992, respectively. He was with the Institute of Flexible Automation at the Technische Universität Wien for one year and then joined the Institute for Microelectronics, where he is currently an associate professor. He received the venia docendi in microelectronics in 1998. In the summer of 1993, he was a visiting scientist at Motorola Inc., Austin, Texas, and in the summer of 1999, a visiting scientist at Intel Corp., Santa Clara, California. Dr. Kosina served as a Technical Program Committee member in the IEEE International Workshop on Computational Electronics in 2003 and 2004 and was chairman of the ''11th International Workshop on Computational Electronics'' held in Vienna in May 2006. He has served as the Associate Editor of the IEEE Transactions on Computer-Aided Design of Circuits and Systems since January 2004. His current research interests include the device modeling of semiconductor devices, nanoelectronic devices, organic semiconductors and optoelectronic devices, the development of novel Monte Carlo algorithms for classical and quantum transport problems, and computer-aided engineering in ULSI-technology.
Modeling Electron-Electron Scattering in Semiconductors
It is commonly accepted that electron-electron scattering (EES) alters the high-energy tail of the energy distribution function. Since physical models of hot-carrier degradation of semiconductor devices rely on an accurate description of the distribution function, it is important to model the effects of EES carefully.
The Boltzmann collision operator, taking into account electron-electron scattering (EES), is nonlinear in the single-particle distribution function. A numerical solution of the resulting nonlinear Boltzmann equation thus requires an iterative method. In terms of the two-particle distribution function, however, the scattering operator is linear. We have formulated a kinetic equation for the two-particle distribution function and derived Monte Carlo (MC) algorithms for the numerical solution of that equation.
The stationary transport problem for a uniform electric field is solved by a two-particle MC algorithm. A pair of trajectories is traced for a long period of time and quantities of interest can be computed by several methods: Time-averaging, sampling at equidistant time steps and before-scattering sampling. The energy distribution functions of electrons in bulk silicon have been calculated. The nonequlibrium distributions are broadened due to EES especially at low temperatures. The transient transport problem for a bulk semiconductor is solved by an ensemble MC algorithm. The time evolution of an ensemble of particle pairs is computed, and quantities of interest are obtained as ensemble averages.
As a transient problem, we analyzed the mixing of a hot and a cold carrier ensemble. The energy of the hot ensemble relaxes faster in the presence of EES, whereas the cold ensemble is temporarily heated by EES (see Fig. 1). Recently, the stationary two-particle algorithm has been extended to non-uniform electric fields. We studied the energy distributions in an n-i-n diode. At room temperature, a moderate enhancement of the high energy tail due to EES is observed. The novelty of the proposed method is that the problem to be solved is linear. Storing and iteratively updating the single-particle distribution is not required.
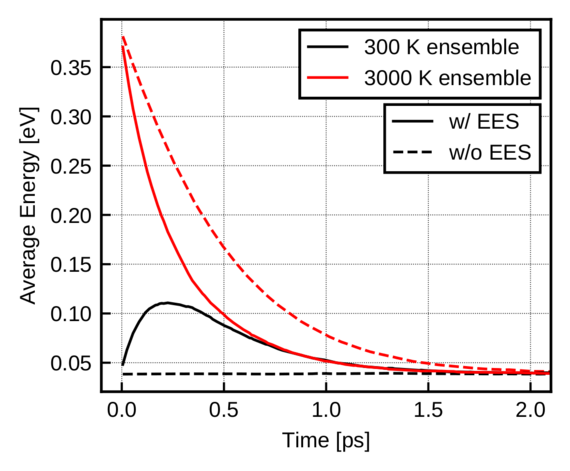
Fig. 1: Dashed curve: Energy relaxation due to electron-phonon scattering in silicon at 300 K. The solid line shows a stronger energy relaxation for the hot-carrier ensemble due to EES. The mean energy of the cold ensemble is temporarily increased. The initial two-particle distribution function assumed is a product of a cold Maxwellian at 300 K and a heated Maxwellian at 3000 K.



