C.2 RF Performance

For high-frequency application of MESFETs, an important figure of merit is the cutoff frequency $f_\mathrm{t}$, which is the frequency at which the MESFET can no longer amplify the input signal. The small-signal input current $\widetilde{i}_\mathrm{in}$ is the product of the gate admittance and the small-signal gate voltage $\widetilde{i}_\mathrm{in}$, assuming that the device has negligibly small series resistance

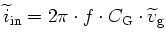$$\widetilde{i}_\mathrm{in}=2\pi \cdot f \cdot C_{\mathrm{G}} \cdot \widetilde{v}_\mathrm{g}$$ (C.12)

where $C_\mathrm {G}$ is the gate capacitance equals to $W\cdot L_\mathrm{g}\cdot(\varepsilon_s/\overline{W})$ and $\overline{W}$ is the average depletion-layer width under the gate electrode, and $\widetilde{v}_\mathrm{g}$ is the small-signal gate voltage. From the definition of the transconductance [37]

$$g_{\mathrm{m}} = \displaystyle\frac{\mathrm{d}I_\mathrm{c}}{\math... ...}}=\displaystyle\frac{\widetilde{i}_{\mathrm{out}}}{\widetilde{v}_{\mathrm{g}}}$$ (C.13)

the output current becomes

$$\widetilde{i}_\mathrm{out}=g_{\mathrm{m}} \cdot \widetilde{v}_{\mathrm{g}}.$$ (C.14)

From (C.12) and (C.14) where $\widetilde{i}_\mathrm{out}=\widetilde{i}_\mathrm{in}$ , becomes

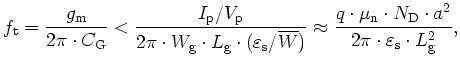$$f_\mathrm{t}=\displaystyle\frac{g_\mathrm{m}}{2\pi \cdot C_\mathr... ... N_\mathrm{D}\cdot a^2}{2\pi \cdot \varepsilon_\mathrm{s}\cdot L^2_\mathrm{g}},$$ (C.15)

From (C.15) one can see that to improve high-frequency performance, a MESFET with high carrier mobility and short channel length should be used. This is the reason that n-channel SiC MESFET, which has a higher electron mobility, is preferred.

The derivation in (C.15) is based on the assumption that the carrier mobility in the channel is a constant, independent of the electric field. However, for very high-frequency operations, the longitudinal field, i.e., the electric field direct from the source to the drain, is sufficiently high that the carriers travel at their saturation velocity.

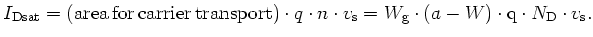$$I_\mathrm{Dsat} =(\mathrm{area}\,\mathrm{for}\,\mathrm{carrier}\,... ...= W_\mathrm{g}\cdot(a-W)\cdot {\mathrm{q}}\cdot N_\mathrm{D}\cdot v_\mathrm{s}.$$ (C.16)

The transconductance is then

$$g_{\mathrm{m}}=\frac{\mathrm{d}I_\mathrm{Dsat}}{\mathrm{d}V_\math... ...isplaystyle\frac{W_\mathrm{g}\cdot v_\mathrm{s}\cdot\varepsilon_\mathrm{s}}{W}.$$ (C.17)

The value of $\mathrm{d}W/\mathrm{d}V_\mathrm{G}$ is obtained from (C.5). Finally, from (C.17), we can obtain the cutoff frequency under saturation velocity condition:

$$f_\mathrm{t}=\displaystyle\frac{g_\mathrm{m}}{2\pi \cdot C_\mathr... ...silon_\mathrm{s}/W)}=\displaystyle\frac{v_\mathrm{s}}{2\pi \cdot L_\mathrm{g}}.$$ (C.18)

Therefore, to increase $f_\mathrm{t}$, we must reduce the gate length $L_\mathrm{g}$ and employ a semiconductor with a high velocity. SiC is superior to other semiconductor materials to operate at higher cutoff frequency due to its higher electron drift velocity.

T. Ayalew: SiC Semiconductor Devices Technology, Modeling, and Simulation