previous up next Dissertation Tesfaye Ayalew contents
 Previous: 2.1.1 Crystallography   Up: 2.1 SiC Material Properties   Next: 2.2 SiC Device Applications


2.1.2 Electrical Properties

Owing to the differing arrangement of Si and C atoms within the SiC crystal lattice, each SiC polytype exhibits unique fundamental electrical and optical properties. Some of the more important electrical properties of the 3C-, 4H-, and 6H-SiC polytypes are given in Table 2.3. Much more detailed electrical properties can be found in [35,36] and references therein. Even within a given polytype, some important electrical properties are non-isotropic, in that they strongly depend on the crystallographic direction of the current flow and the applied electric field (for example, electron mobility for 6H-SiC).

Table 2.3: Comparison of electrical properties of SiC polytypes with Si [37,35,36].
  Si 4H-SiC 6H-SiC 3C-SiC
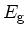Bandgap energy $ E_{\mathrm{g}}$
[eV]
1.12 3.26 3.03 2.4
Relative dielectric
constant  $ \varepsilon_\mathrm{s}$
11.9 9.7 9.66 9.72
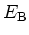Breakdown Field $ E_\mathrm{B}$
@ N$ _{D}$=10$ ^{17}$cm$ ^{-3}$[MV/cm]
0.3 $ \parallel $c-axis: 3.0
$ \parallel $c-axis: 3.2
$ \perp $c-axis: $ > 1$
$ > 1.5$
Thermal Conductivity
$ \kappa$ [W/cmK]
1.31 4.9 4.9 3.2
Intrinsic Carrier
Concentration $ n_\mathrm{i}$[cm$ ^{-3}$]
9.65 $ \times 10^{9}$ 5 $ \times 10^{-9}$ 1.6 $ \times 10^{-6}$ 1.5 $ \times 10^{-1}$
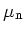Electron Mobility $ \mu_\mathrm{n}$
@ N$ _{D}$=10$ ^{16}$cm$ % ^{-3} $[cm$ ^{2}$/Vs]
1430
$ \parallel $c-axis: 900
$ \perp $c-axis: 800
$ \parallel $c-axis: 60
$ \perp $c-axis: 400
800
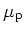Hole Mobility $ \mu_\mathrm{p}$
@ N$ _{A}$=10$ ^{16}$cm$ % ^{-3} $[cm$ ^{2}$/Vs]
480 115 90 40
Saturated Electron
Velocity $ v$[10$ ^{7}$cm/s]
1 2 2 2.5
Donors & Ionization
Energy $ \Delta E_\mathrm{d}$[meV]
P: 45
As: 54
N: 50, 92
P: 54, 93
N: 85, 140
P: 80, 110
N: 50
Acceptors & Ionization
Energy $ \Delta E_\mathrm{a}$[meV]
B: 45
Al: 67
Al: 200
B: 285
Al: 240
B: 300
Al: 270
2003 Commercial
Wafer Diameter [inches]
12 3 3 $ ?$



For comparison, Table 2.3 also includes comparable properties of silicon. To varying degrees the major SiC polytypes exhibit advantages and disadvantages in basic material properties compared to silicon. Three key categories where SiC enjoys inherent advantages over Si for high-temperature operation are the thermal conductivity, the electric field breakdown strength, and the energy bandgap (E $ _\mathrm{g}$). SiC has 3 to 13 times higher thermal conductivity than Si at 300 K, an approximately three times wider, while still possessing a saturation velocity ( $ v_\mathrm{sat}$) of 2$ \times$ l0$ ^7$ cm s$ ^{-1}$ [38].


All of the quantities shown in Table 2.3 are temperature dependent to differing extent. The low, anisotropic electron mobility in 6H-SiC is one of the primary reasons for the emerging popularity of 4H-SiC which has a higher and much less anisotropic electron mobility. In fact $ \mu_\perp$/ $ \mu_\parallel$ is about 0.8 at 300K in 4H-SiC, while the same ratio is about 5 in 6H-SiC [38].


The intrinsic carrier concentration ($ n_i$) is directly proportional to N$ _C$ and N$ _V$, which are the conduction band and valence band density of states, respectively. However, as a result of thermal expansion of the lattice and electron-phonon coupling, $ n_i$ has an exponential dependence upon temperature, as well as E $ _\mathrm{g}$. The intrinsic carrier concentration is important in high-temperature device applications, because pn junction leakage currents in devices are normally proportional to n$ _i$ or n$ _i^2$ (Subsection 2.2.1). Electron effective masses ($ m^*_\perp$ = 0.42 m$ _0$ and $ m^*_\parallel$ = 0.39 m$ _0$ in 4H-SiC [36]) have not been analyzed as a function of temperature. Typical bandgap values are obtained from photoluminescence studies performed at liquid He temperatures ($ \sim $4.2K) under very low pressures ($ \sim $10$ ^{-11}$ T) [35]. High doping levels lead to band gap narrowing (BGN) effects in semiconductors, but have not been extensively studied in SiC, so the effective intrinsic carrier concentration ($ n_{ie}$) relationship with doping has not been established.


Dopants in SiC can be incorporated into energetically inequivalent quasi-hexagonal ($ h$) C-sites or Si-sites, or quasi-cubic ($ k$) C-sites or Si-sites (only Si sites are $ h$ or $ k$ labeled in Fig. 2.3). While all dopant ionization energies associated with various dopant incorporation sites should normally be considered for utmost accuracy, Table 2.3 lists only the shallowest ionization energies of each impurity. The arrangement of next neighbors in the lattice is the same for all SiC polytypes, but crystallographically inequivalent lattice sites exist in different polytypes. Thus, electronic properties, such as effective mass, carrier mobility ($ \mu$), and bandgap, vary widely between different polytypes of SiC.


Electrically active impurities in semiconductors are normally substitutional dopants, occupying vacant lattice sites. Dopants for SiC include N (n-type), and Al, B, Be, Ga, O, and Sc (p-type), with Al being the most common p-type dopant, because it has the shallowest acceptor level [35]. Undoped SiC is typically n-type from residual nitrogen, and has a slight green tint in color for 6H-SiC. The color of the material depends upon the specific polytype, however. Donor activation energies are often found to vary over a wide range, depending upon the measurement technique, material quality, polytype and dopant concentrations. Activation energies also vary depending upon the substitutional site occupied in the lattice (cubic or hexagonal). For n-type 3C-SiC, Hall measurements have yielded nitrogen activation energies from 50meV. In 6H-SiC, two donor levels have been found depending upon the occupancy site. The hexagonal site is 85meV, and the cubic site is 140meV [36]. In 4H-SiC material, donor levels are 50meV, and 92meV for hexagonal and cubic sites, respectively [35]. The fact that most dopant levels are deeper than those found comparably in silicon explains the partial carrier freeze-out found in SiC at room temperature, since the thermal energy ( $ {\mathrm{k_B}}T$/ $ {\mathrm{q}}$) is only $ \sim25.9$meV at 300K. Despite this, SiC junction field effect transistors (JFETs) have been operated to temperatures as low as 77K, because of field ionization of dopants. In contrast, for p-type Al doped SiC, an average acceptor energy level of approximately from 200 to 240meV is found for all polytypes [36]. Other p-type dopants such as boron have deeper acceptor levels (approximately 300meV), and are not as commonly used.


previous up next   contents
 Previous: 2.1.1 Crystallography   Up: 2.1 SiC Material Properties   Next: 2.2 SiC Device Applications
T. Ayalew: SiC Semiconductor Devices Technology, Modeling, and Simulation