3.6.1 Eigenvalues of a Triangular Energy Well

To first order the conduction band edge in a MOSFET inversion layer can be approximated by a linear potential (this is actually done by various authors, see [161,162,163,164]). The solution of SCHRÖDINGER's equation for a linear potential has been derived in Section 3.5.2 and consists of a linear superposition of AIRY's functions. If the triangular energy well is defined as

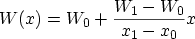$$W(x) = W_0 + \frac{W_1 - W_0}{x_1 - x_0} x$$ (3.94)

and no wave function penetration for $x <= x_0$ is taken into account, the wave function for $x>0$ can be written as [156]

$$\Psi(x) = A \ensuremath{\mathrm{Ai}}(u(x)) \ ,$$ (3.95)

$$\Psi(x_0) = A \ensuremath{\mathrm{Ai}}(u(x_0)) = 0 \ .$$ (3.96)

Therefore, $u(x_0)$ must equal one of the zeros of the AIRY function $z_i$:

$$u(x_0) = z_i < 0 \ .$$ (3.97)

With $u(x)$ from expression (3.68) the energy eigenvalues are found as

$${\mathcal{E}}_i = W_0 - z_i \left( \frac{\hbar^2}{2m} \right)^{1/3} \left( \frac{W_1 - W_0}{x_1 - x_0}\right)^{2/3} \ .$$ (3.98)

The first five zeros of the AIRY function are $-2.34$, $-4.09$, $-5.52$, $-6.79$, and $-7.94$. These values are often used to approximate the quantized carrier concentration in the channel of MOS devices. The value of the normalizing constant $A$ becomes (the derivation is shown in Appendix C)

$$A = \left( \frac{\left( \displaystyle\frac{2m\ensuremath {\mathrm... ...\lambda_0) - \lambda_0 \ensuremath{\mathrm{Ai}}^2(\lambda_0)} \right)^{1/2} \ ,$$ (3.99)

where $E$ is the constant electric field in the energy well, and the value of $\lambda_0$ depends on the energy eigenvalue ${\mathcal{E}}_i$ via

$$\lambda_0 = - \frac{{\mathcal{E}}_i}{\ensuremath {\mathrm{q}}E} \left( \frac{2m\ensuremath {\mathrm{q}}E}{\hbar^2} \right)^{1/3} \ .$$ (3.100)

This method can be used to get an estimate of the first few eigenvalues of the system, or to find initial values for the calculation of the eigenvalues described in the next section. A. Gehring: Simulation of Tunneling in Semiconductor Devices