next up previous contents
Next: 2.3.3.2 Resistor Up: 2.3.3 Devices Previous: 2.3.3 Devices

2.3.3.1 Conductor

The constitutive relations for a linear, temperature dependent conductor are

I = V . G($\displaystyle \vartheta$) (2.29)
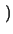G($\displaystyle \vartheta$) = G0 . $\displaystyle \left(\vphantom{ 1 + \alpha \cdot (\vartheta - \vartheta_{\mathit{ref}}) }\right.$1 + $\displaystyle \alpha$ . ($\displaystyle \vartheta$ - $\displaystyle \vartheta_{\mathit{ref}}^{}$)$\displaystyle \left.\vphantom{ 1 + \alpha \cdot (\vartheta - \vartheta_{\mathit{ref}}) }\right)$ (2.30)
P = V . I (2.31)

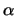
If $ \alpha$$ \ne$ 0, the conductor will be modeled temperature dependently. For thermal simulation the dissipated power P will result in self-heating of the conductor and the problem becomes non-linear. Otherwise the temperature dependent entries are ignored. The stamp is given as
yx, y 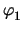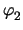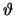$ \varphi_{1}^{}$ $ \varphi_{2}^{}$ $ \vartheta$ f
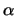n1 G - G - V . $ \alpha$ . G0 - I
n2 - G G V . 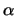$ \alpha$ . G0 I
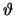$ \vartheta$ -2 . V . G    2 . V . G     - V2 . 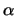$ \alpha$ . G0 P

Figure 2.5: Electro-thermal compound model for a heat dissipating resistor
\begin{figure} \begin{center} \resizebox{7.8cm}{!}{ \psfrag{n-term}{\hspace*{-1.... ... \includegraphics[width=7.8cm,angle=0]{figures/res.eps}}\end{center}\end{figure}

The conductor acts as a heat source connected to the thermal circuit node 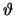$ \vartheta$ and to thermal ground (reference temperature).

next up previous contents
Next: 2.3.3.2 Resistor Up: 2.3.3 Devices Previous: 2.3.3 Devices
Tibor Grasser
1999-05-31