



Next: Appendix B: STL Iterator Analysis
Up: 4 Applied Concepts
Previous: 10. Summary and Outlook
Appendix A: Common Mathematical Terms
Basic mathematical terms are reviewed. The readers' familiarity with
sets and subsets [2] is required in the
following. All sets which contain only one element (singleton) can be
used to describe a vertex.
Figure:
A relation  of a set
of a set  and a set
and a set  .
.
![\begin{figure}\begin{center}
\small\psfrag{A} [c]{{\ensuremath{A}}}\psfrag{B...
...e=figures/relation_function.eps, width=0.35\textwidth}\end{center}\end{figure}](img901.png) |
A permutation of a finite set is usually given by its action on the
elements of the set. An example is given by the basic set
 with a transformation into
with a transformation into
 where the notation states that the permutation
maps
where the notation states that the permutation
maps
 ,
,
 and so on. Thereby all
permutations of a finite set can be placed into two sets.
and so on. Thereby all
permutations of a finite set can be placed into two sets.
Definition 46 (Parity)
A permutation of a finite set can be expressed as either an even or an
odd number of transpositions, but not both. In the former case, the
permutation is called even, in the latter it is odd.
Figure:
The image of  under
under  .
.
![\begin{figure}\begin{center}
\small\psfrag{A} [c]{{\ensuremath{A}}}\psfrag{B...
...gure=figures/relation_image.eps, width=0.35\textwidth}\end{center}\end{figure}](img911.png) |
Definition 49 (Preimage)
The preimage (fiber, inverse image) of a set
 under
under
 is the subset of
is the subset of
 defined by
defined by
The preimage of a singleton,
 , is a fiber or a level set.
A fiber can also be the empty set
, is a fiber or a level set.
A fiber can also be the empty set  . The union set of all
fibers of a function is called the total space, E.
. The union set of all
fibers of a function is called the total space, E.
Definition 51 (Abelian)
A group  is Abelian, if its binary operation
is Abelian, if its binary operation  is commutative.
is commutative.
Definition 56 (Vector Space)
A vector space
 over a field
over a field
 is a set associated
with two binary operations. The elements of
is a set associated
with two binary operations. The elements of
 are called
vectors, while the elements of
are called
vectors, while the elements of
 are called scalars. The
binary operations are addition
are called scalars. The
binary operations are addition
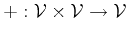 |
(11.3) |
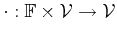 |
(11.4) |
 is closed under
its two binary operations.
is closed under
its two binary operations.
Definition 57 (Linear Mapping)
A mapping
 is called linear,
if the following relation holds
is called linear,
if the following relation holds
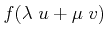 |
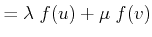 |
(11.5) |
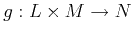 |
(11.6) |
The extension of this notion to more than two arguments is called a multi-linear mapping.
Figure:
The kernel of  .
.
![\begin{figure}\begin{center}
\small\psfrag{G} [c]{G}\psfrag{G'} [c]{G'}\ps...
...gure=figures/relation_kernel.eps, width=0.5\textwidth}\end{center}\end{figure}](img960.png) |




Next: 12. STL Iterator Analysis
Up: 4 Applied Concepts
Previous: 10. Summary and Outlook
R. Heinzl: Concepts for Scientific Computing
![]() with a transformation into
with a transformation into
![]() where the notation states that the permutation
maps
where the notation states that the permutation
maps
![]() ,
,
![]() and so on. Thereby all
permutations of a finite set can be placed into two sets.
and so on. Thereby all
permutations of a finite set can be placed into two sets.