


 Previous: 6.2.3 Operator-Theoretic Structure
Up: 6.2 Quantum Mechanics in
Next: 6.2.5 A Caveat on
Previous: 6.2.3 Operator-Theoretic Structure
Up: 6.2 Quantum Mechanics in
Next: 6.2.5 A Caveat on
The standard semantics of quantum mechanics as specified by the
Kopenhagen interpretation is a probabilistic one. The probabilistic
structure manifests itself as inner product in a Hilbert space:
The space of operators with the trace as inner product is a Hilbert space.
The operator product has already been translated to phase space in the
preceding section. Now we come to the translation of the
inner product.
The expectation value  of an operator
of an operator  in a state
in a state
 is given
by performing the trace operation:
is given
by performing the trace operation:
 |
(6.52) |
In phase space the trace becomes a simple integral over the
ordinary product of the corresponding
Weyl transforms:
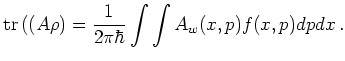 |
(6.53) |
Therefore, the computation of average values takes the same
form as in classical statistical mechanics, with the
Weyl transform  and the Wigner function
and the Wigner function  playing the
roles of the classical observable
playing the
roles of the classical observable  and the classical
probability distribution
and the classical
probability distribution  respectively.
respectively.
 or
or  projection leads to marginal probability densities:
a space like shadow
projection leads to marginal probability densities:
a space like shadow
 or else
a momentum-space shadow
or else
a momentum-space shadow
 . Both
are (bona-fide) probability densities, being positive semidefinite,
as they are the expectation values of the projection operators
on the corresponding eigenstates.
. Both
are (bona-fide) probability densities, being positive semidefinite,
as they are the expectation values of the projection operators
on the corresponding eigenstates.
But neither can be conditioned on the other, as the uncertainty
principle is fighting back: The Wigner function itself can, and
most often becomes negative in some areas of phase space.
In fact, the only pure-state Wigner function which is non-negative
is the Gaussian.



 Previous: 6.2.3 Operator-Theoretic Structure
Up: 6.2 Quantum Mechanics in
Next: 6.2.5 A Caveat on
Previous: 6.2.3 Operator-Theoretic Structure
Up: 6.2 Quantum Mechanics in
Next: 6.2.5 A Caveat on
R. Kosik: Numerical Challenges on the Road to NanoTCAD
![]() of an operator
of an operator ![]() in a state
in a state
![]() is given
by performing the trace operation:
is given
by performing the trace operation:
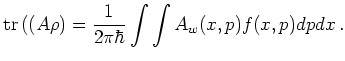
![]() or
or ![]() projection leads to marginal probability densities:
a space like shadow
projection leads to marginal probability densities:
a space like shadow
![]() or else
a momentum-space shadow
or else
a momentum-space shadow
![]() . Both
are (bona-fide) probability densities, being positive semidefinite,
as they are the expectation values of the projection operators
on the corresponding eigenstates.
. Both
are (bona-fide) probability densities, being positive semidefinite,
as they are the expectation values of the projection operators
on the corresponding eigenstates.
![]()
![]()
![]()
![]() Previous: 6.2.3 Operator-Theoretic Structure
Up: 6.2 Quantum Mechanics in
Next: 6.2.5 A Caveat on
Previous: 6.2.3 Operator-Theoretic Structure
Up: 6.2 Quantum Mechanics in
Next: 6.2.5 A Caveat on