Next: 3.2 Theory
Up: 3. The Effect of
Previous: 3. The Effect of
Organic semiconductors can be considered as hopping networks and are
characterized by strong disorder in both energy and space [8,9]. This makes
it very difficult to solve the problem analytically or simulate the
carrier transport and recombination in such a system by starting from a
one-particle master equation. Consequently, an analytical approach to this
problem is normally based on a specific set of assumptions and
simplifications [20,68]. The concept of transport energy is a very
useful tool for the analysis of charge
hopping transport in organic semiconductors. The importance of the transport energy
stems from the fact that it maximizes the probability for a carrier to hop upward. It does not
depend on the initial energy of the carrier and serves as an analog of
the mobility edge [10].
The transport energy concept is based on the Miller-Abrahams expression
[7,71]. This equation can be written as
 |
(3.1) |
For a particular density of states
, the transport
energy can be obtained in the following way [10]. For an electron with
energy 
, the median rate of a upward hop to a
neighboring localized state with energy 
is
 |
(3.2) |
where
The transport energy can be calculated by maximizing the rate (3.2) with
respect to the final energy 
 |
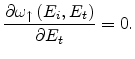(3.3) |
After some calculation we obtain
![$\displaystyle g\left(E_t\right)\left[\int_\infty^{E_t} g\left(E\right)dE\right]^{-4/3}=\frac{1}{\alpha k_BT}\left(\frac{9\pi}{2}\right)^{1/3}.$](img323.png) |
(3.4) |
Here we can see that the transport energy does not depend on the
initial energy . The transport energy has been extended to an exponential
DOS in [10] and later to a Gaussian DOS in [77].
Next: 3.2 Theory
Up: 3. The Effect of
Previous: 3. The Effect of
Ling Li: Charge Transport in Organic Semiconductor Materials and Devices
![$\displaystyle R\left(E_t\right)=\left[\frac{4\pi}{3}\int_{-\infty}^{E_t}
g\left(E\right)dE\right]^{-1/3}$](img321.png)