4.2 Theory

For a disordered organic semiconductor system, we assume that localized states are randomly distributed in both the energy and the coordinate space, and that they form a discrete array of sites. Conduction proceeds via hopping between these sites. In the case of low electric field, the conductivity between site $i$ and site $j$ can be calculated as [17,44]

$$\sigma_{ij}\approx\gamma\exp\left(-2\alpha R_{ij}-\frac{\mid E_i-E_F\mid+\mid E_j-E_F\mid+\mid E_i-E_j\mid}{2k_BT}\right)$$ (4.1)

where $E_i$ and $E_j$ are the energies at the sites $i$ and $j$, respectively, $E_F$ is the Fermi-energy, $R_{ij}$ is the distance between sites $i$ and $j$, and $\alpha^{-1}$ is the Bohr radius of the localized wave function. The first term $2\alpha R_{ij}$ is a tunneling term, and the second one is a thermal activation term (Boltzman term).

For organic semiconductors, the manifolds of both the lowest unoccupied molecular orbitals (LUMO) and the highest occupied molecular orbitals (HOMO) are characterized by random positional and energetic disorder. Being embedded into a random medium, similarly, dopant atoms and molecules are inevitably subjected to the positional and energetic disorder, too. Since the HOMO level in most organic semiconductors is deep and the gap separating LUMO and HOMO states is wide, energies of donor and acceptor molecules are normally well below LUMO and above HOMO. So we assume a double exponential density of states

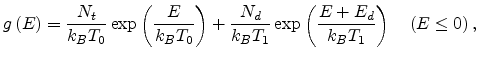$$g\left(E\right)=\frac{N_t}{k_BT_0}\exp\left(\frac{E}{k_BT_0}\righ... ...frac{N_d}{k_BT_1}\exp\left(\frac{E+E_d}{k_BT_1}\right)\quad\left(E\leq0\right),$$ (4.2)

where $N_t$ and $N_d$ are the concentrations of the intrinsic and the dopant states, respectively, $T_0$ and $T_1$ are parameters indicating the widths of the intrinsic and the dopant distributions, respectively, and $E_d$ is the Coulomb trap energy [92]. Vissenberg and Matters [43] pointed out that they do not expect the results to be qualitatively different for a different choice of $g\left(E\right)$, as long as $g\left(E\right)$ increases strongly with $E$. Therefore, we assume that transport takes place in the tail of the exponential distribution.

The equilibrium distribution of carriers $\rho\left(E\right)$ is determined by the Fermi-Dirac distribution $f\left(E\right)$ as follows

$$\rho\left(\epsilon\right)= g\left(E\right)f\left(E\right)=\frac{g\left(E\right)}{1+ \exp\left[\left(E-E_F\right)/{k_BT}\right]}.$$

The Fermi-energy of this system is fixed by the equation for the carrier concentration $n$,

$$n=\int\frac{d\epsilon g\left(E\right)}{1+\exp\left(\frac{E-E_F}{k_BT}\right)}=n_t+n_d$$ (4.3)

where

$$n_t=N_t\exp\left(\frac{\epsilon_F}{K_BT_0}\right)\Gamma\left(1-T/T_0\right)\Gamma\left(1+T/T_0\right)$$

$$n_d=N_d\exp\left(\frac{\epsilon_F-E_d}{K_BT_1}\right)\Gamma\left(1-T/T_1\right)\Gamma\left(1+T/T_1\right)$$

Here, $\Gamma$ is the gamma function. According to the classical percolation theory [17], the current will flow through the bonds connecting the sites in a random Miller and Abrahams network [9]. The conductivity of this system is determined when the first infinite cluster occurs. At the onset of percolation, the critical number $B_c$ can be written as

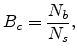$$B_c=\frac{N_b}{N_s},$$ (4.4)

where $B_c=2.8$ for a three-dimensional amorphous system, $N_b$ and $N_s$ are, respectively, the density of bonds and the density of sites in this percolation system, which can be calculated by [43,93,94].

$$N_b=\int d{\bf {R}}_{ij}dE_idE_jg\left(E_i\right)g\left(E_j\right)\theta\left(s_c-s_{ij}\right),$$ (4.5)

$$N_s=\int dE g\left(E\right)\theta\left(s_ck_BT-\mid E-E_F\mid\right).$$ (4.6)

Here ${\bf R_{ij}}$ denotes the distance vector between sites $i$ and $j$, $\theta$ is the unit step function, and $s_c$ is the exponent of the conductance given by the relation [19]

$$\sigma=\sigma_0\exp\left(-s_c\right).$$ (4.7)

Substituting (4.2), (4.5) and (4.6) into (4.4), we obtain the expression,

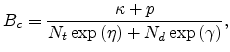$$B_c=\frac{\kappa+p}{N_t\exp\left(\eta\right)+N_d\exp\left(\gamma\right)},$$ (4.8)

where

$$\kappa=\pi N_t^2\psi^3\exp\left(2\eta\right)+\pi N_d^2\xi^3\exp\left(2\gamma\right),$$

$$p=\frac{\pi}{4} N_tN_d\exp\left(\eta+\gamma\right)\left(\psi^{-1}+\xi^{-1}\right)^{-3},$$

$$\eta=\frac{E_F+k_BTs_c}{k_BT_0},\qquad\gamma=\frac{E_F-E_d+k_BTs_c}{k_BT_1},$$

$$\psi=\frac{T_0}{4\alpha T},\qquad\xi=\frac{T_1}{4\alpha T}.$$

Equation (4.8) has been obtained under the following conditions:

• the site positions are random,
• the energy barrier for the critical hop is large compared with $k_BT$,
• and the carrier concentration is very low.

The exponent $s_c$ is obtained by a numerical solution of (4.8) and the conductivity can be calculated using (4.7).