6.3.2 Resistance and Thermal Simulation

A current will flow between any pair of contacts at different electrical potential (in a conductive material). Each electrically isolated conductor can be treated as an individual problem whose solution involves solving an equation similar to (6.1) to calculate the current density and potential distribution. From those results, the resistance is extracted using Ohm's law.

If $\gamma_E$ denotes the electrical conductivity (assumed to be $0$ in all non-conductor materials), we obtain

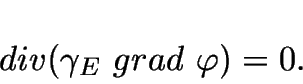$$div(\gamma_E~grad~\varphi)=0.$$ (6.2)

For the thermal problem the resolution of

$div(\gamma_T~grad~T)=-p$

is required in all simulation domains. Here $\gamma_T$ represents the thermal conductivity, $T$ is the temperature distribution and $p=\gamma_E~(grad~\varphi)^2$ is the power loss density.

The electrical and thermal equations are linked by a first order approximation given by

$\gamma_E=\gamma_0~\frac{1}{1+\alpha~(T-T_0)}$

where $\alpha$ is a constant temperature coefficient and $\gamma_0$ is the electric conductivity at room temperature $T_0$.