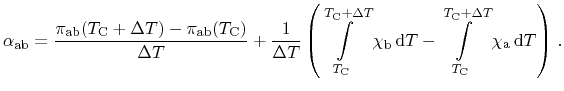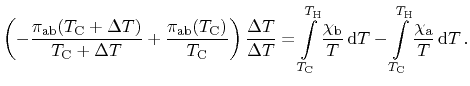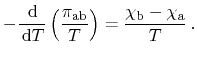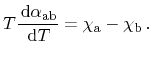2.1.4 Thermodynamic Relations

As already indicated, the three thermoelectric effects are not independent from each other and thus the according coefficients are related. In the sequel, these relations are discussed on the basis of fundamental thermodynamics [9,10,11].

While all three effects describe reversible phenomena, further two irreversible processes occur within the structure. First, each electrical current causes the dissipation of Joule heat when passing a material with a certain electrical resistance. Second, heat is conducted within the device as described by Fourier's law.

In the following derivations, the device illustrated in Fig. 2.1 is considered as electrically short-circuited for the sake of brevity. Thus, no external electric voltage is induced and no electric power is dissipated. Furthermore, the cold and the hot contact are connected to thermal reservoirs. Energy losses by Joule heating are very small and can be safely neglected. Considering all three thermoelectric effects, the application of total energy conservation within the entire device including the reservoirs for a closed loop reads

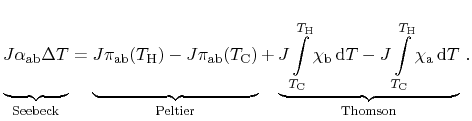$$\underbrace{\vphantom{\int_{\ensuremath{T_{\mathrm{C}}}}^{\ensure... ...}_\ensuremath{\mathrm{a}} \d\ensuremath{T}}_{\ensuremath{\mathrm{Thomson}}} \,.$$ (2.10)

There, the Seebeck effect maintains a driving force causing a current running throughout the device. This current itself induces the Peltier effect as well as the Thomson effect. Introducing the temperature difference $\Delta \ensuremath{T}$ as $\ensuremath{T_{\mathrm{H}}}-\ensuremath{T_{\mathrm{C}}}$ and dividing (2.10) by $\Delta \ensuremath{T}$ as well as $J$ results in

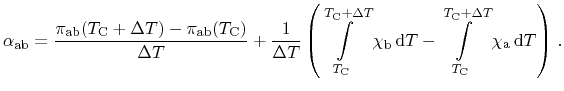$$\ensuremath{\alpha}_\ensuremath{\mathrm{ab}} = \frac{\ensuremath{... ...emath{T}} \ensuremath{\chi}_\ensuremath{\mathrm{a}} \d\ensuremath{T}\right) \,.$$ (2.11)

Letting $\Delta \ensuremath{T}$ approach zero, the energy relation between the three effects is obtained

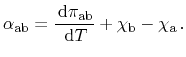$$\ensuremath{\alpha}_\ensuremath{\mathrm{ab}} = \frac{\d\ensuremat... ...h{\chi}_\ensuremath{\mathrm{b}} - \ensuremath{\chi}_\ensuremath{\mathrm{a}} \,.$$ (2.12)

Next, the net change of entropy of the entire structure including the heat reservoirs can be assumed to be zero due to the neglect of irreversible processes. Accordingly, contributions from all three effects cancel

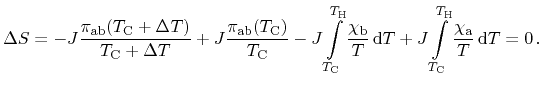$$\Delta \ensuremath{S}= -J \frac{\ensuremath{\pi}_\ensuremath{\mat... ...suremath{\chi}_\ensuremath{\mathrm{a}}}{\ensuremath{T}} \d\ensuremath{T}= 0 \,.$$ (2.13)

Division of (2.13) by $J$ as well as extending the Peltier term by $\Delta \ensuremath{T}/\Delta \ensuremath{T}$ results in

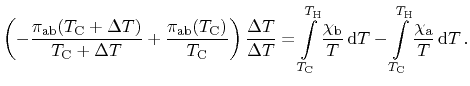$$\left( -\frac{\ensuremath{\pi}_\ensuremath{\mathrm{ab}}(\ensurema... ...{\ensuremath{\chi}_\ensuremath{\mathrm{a}}}{\ensuremath{T}} \d\ensuremath{T}\,.$$ (2.14)

Again letting $\Delta \ensuremath{T}$ approach zero, the relation between Peltier and Thomson coefficients is obtained as

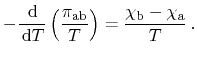$$- \frac{\d}{\d\ensuremath{T}} \left(\frac{\ensuremath{\pi}_\ensur... ...math{\mathrm{b}}-\ensuremath{\chi}_\ensuremath{\mathrm{a}}}{\ensuremath{T}} \,.$$ (2.15)

Expansion of the derivative yields a more convenient formulation

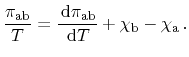$$\frac{\ensuremath{\pi}_\ensuremath{\mathrm{ab}}}{\ensuremath{T}} ... ...h{\chi}_\ensuremath{\mathrm{b}} - \ensuremath{\chi}_\ensuremath{\mathrm{a}} \,.$$ (2.16)

Inserting (2.12) to (2.16) yields the correlation between Seebeck and Peltier effect, which has already been observed by Thomson and is well known as the first Kelvin relation

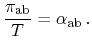$$\frac{\ensuremath{\pi}_\ensuremath{\mathrm{ab}}}{\ensuremath{T}} = \ensuremath{\alpha}_\ensuremath{\mathrm{ab}} \,.$$ (2.17)

Furthermore, substitution of the Peltier term in (2.16) with (2.17) yields the correlation between Seebeck and Thomson coefficients, which is known as the second Kelvin relation

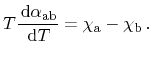$$\ensuremath{T}\frac{\d\ensuremath{\alpha}_\ensuremath{\mathrm{ab}... ...h{\chi}_\ensuremath{\mathrm{a}} - \ensuremath{\chi}_\ensuremath{\mathrm{b}} \,.$$ (2.18)

The same result can be obtained from Onsager's reciprocal relations of irreversible thermodynamics [12] which are a cornerstone within the description of linear irreversible processes and are applied in Section 3.5.9 to analyze macroscopic transport models.

M. Wagner: Simulation of Thermoelectric Devices