A. Poisson Brackets Formulation

The Poisson bracket represents an important and convenient operator within Hamiltonian mechanics. It allows not only a compact treatment of the Boltzmann transport equation and its moments as carried in Chapter 3, but has some useful identities applied throughout the derivation of several transport models. Its basic definition for two scalars reads

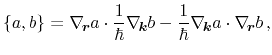$$\ensuremath{\{a,b\}} = \ensuremath{\ensuremath{\ensuremath{\mathi... ...ath{\cdot}\ensuremath{\ensuremath{\ensuremath{\mathitbf{\nabla_{\!r}}}}}{b} \,,$$ (A.1)

whereas the Poisson bracket for a vector valued quantity and a scalar has to be handled more carefully. This case can be extrapolated by having a closer look on its single components. Considering a vector $\ensuremath{\mathitbf{a}}$ with its components $a_x$ , $a_y$ , and $a_z$ , and using Einstein's summation convention

$$\ensuremath{\mathitbf{a}} = \sum_{m=\mathrm{x}}^{\mathrm{z}} a_m \ensuremath{\mathbf{e}}_m = a_m \,,$$ (A.2)

$$\ensuremath{\ensuremath{\ensuremath{\mathitbf{\nabla}}}\ensuremat... ...^{\mathrm{z}} \ensuremath{\partial_{m} a_m} = \ensuremath{\partial_{m} a_m} \,,$$ (A.3)

$$\ensuremath{\ensuremath{\ensuremath{\mathitbf{\nabla}}}\ensuremat... ...{x}}^{\mathrm{z}} \ensuremath{\partial_{n} b_m} = \ensuremath{\partial_{n} b_m}$$ (A.4)

one can write

$$\ensuremath{\{a_m,b\}} = \ensuremath{\ensuremath{\ensuremath{\mat... ...uremath{\cdot}\ensuremath{\ensuremath{\ensuremath{\mathitbf{\nabla_{\!r}}}}}{b}$$ (A.5)

$$= \ensuremath{\partial_{m} a_n} \ensuremath{\frac{1}{\hbar} \part... ...tial_{n}^\ensuremath{\ensuremath{\mathitbf{k}}}a_m} \ensuremath{\partial_{m} b}$$

$$\ensuremath{\{\ensuremath{\mathitbf{a}},b\}} = \ensuremath{\ensur... ...ath{\cdot}\ensuremath{\ensuremath{\ensuremath{\mathitbf{\nabla_{\!r}}}}}{b} \,.$$ (A.6)

With these definitions, the subsequent identities can be carried out. As a consequence of its definition, the Poisson bracket is anti-commutative, meaning that

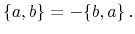$$\ensuremath{\{a,b\}} = - \ensuremath{\{b,a\}} \,.$$ (A.7)

Moreover, the Poisson bracket of a variable with itself vanishes

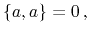$$\ensuremath{\{a,a\}} = 0 \,,$$ (A.8)

which is important for the special case of $\ensuremath{\{\ensuremath{\mathcal{E}},\ensuremath{\mathcal{E}}\}}$ in the following derivations. The Poisson bracket of every scalar or vector and a constant $\ensuremath{C}$ vanishes

$$\ensuremath{\{\ensuremath{C},a\}} = 0 \,,$$ (A.9)

which is especially useful for $\ensuremath{C}= 1$ during the derivation of the balance equations. Furthermore, the Poisson bracket of a product can be expressed as

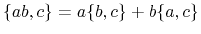$$\ensuremath{\{ab,c\}} = a \ensuremath{\{b,c\}} + b \ensuremath{\{a,c\}}$$ (A.10)

which can be easily verified using the product rule. The Poisson bracket is bi-linear, thus two sums can be expanded like

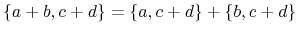$$\ensuremath{\{a+b,c+d\}} = \ensuremath{\{a,c+d\}} + \ensuremath{\{b,c+d\}}$$ (A.11)

$$= \ensuremath{\{a,c\}} + \ensuremath{\{b,c\}} + \ensuremath{\{a,d\}} + \ensuremath{\{b,d\}} \,.$$

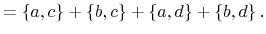M. Wagner: Simulation of Thermoelectric Devices