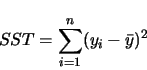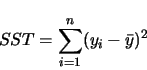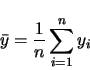3.2.6.1 Observed Data

The total variation in the data values is called the total sum of squares (SST). It is computed by summing the squares of the observed data values with there average value $\bar y$.

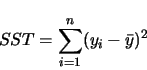$$SST = \sum_{i=1}^n (y_i - \bar y)^2$$ (3.20)

where the average is calculated by

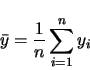$$\bar y = \frac{1}{n} \sum_{i=1}^n y_i$$ (3.21)

and n is the number of data-points. The total sum of squares gives only the variation of the data values and the fitted model has no influence. The degree of freedom associated is n-1.