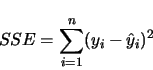3.2.6.3 Residual

The so called sum of squares of the residuals is computed by summing the squares of the observed data with the data of the fitted regression model.

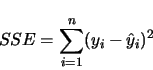$$SSE = \sum_{i=1}^n (y_i - \hat y_i)^2$$ (3.23)

The complete analysis of variance table is shown in Table 3.12. In the row `regression' the degree of freedom (df) and the sum of squares and the estimated mean square of the fitted model and in the next row, the `residual', the values for the difference of the calculated and observed data are listed. The values of F, R², and R_A² from the first row are described later. The last row, `total', holds the sum of squares of the observed data.

Table 3.12: The analysis of variance table.

Source	df	Sum of Squares	Mean Square
Regression	p-1	SSR	$\frac{SSR}{p-1}$
Residual	n-p	SSE	$\frac{SSE}{n-p}$
Total	n-1	SST