4.2 Analytical solution methods for the two-dimensional Helmholtz equation

A solution of (4.13) with $n_{port}$ excitation ports, defined between the cover and the bottom plane (Figure 4.2), relates the port voltages $U_{i}(x_{i},y_{i})$ on the ports with index to the currents $I_{j}(x_{j},y_{j})$ on the ports with index by the impedance matrix $Z_{ij}$ . The coordinates of port i and port j are $(x_{i},y_{i})$ and $(x_{j},y_{j})$ respectively.

$\displaystyle U_{i}(x_{i},y_{i})=\sum_{j=1}^{n_{port}}(Z_{ij}(x_{i},y_{i},x_{j},y_{j})I_{j}(x_{j},y_{j}))$ with $\displaystyle \qquad i=1\ldots n_{port}.$

(4.17)

An analytical solution for rectangular parallel planes with four open edges depicted in Figure 4.2 was presented by [42]. In this solution, the coefficients of the impedance matrix in (4.17) are

$\displaystyle Z_{ij}=\frac{j\omega\mu h}{L_{e}W_{e}}\sum_{m=0}^{\infty}\sum_{n=0}^{\infty}\left[\frac{L_{mn}N_{mni}N_{mnj}}{{k_{m}^2+k_{n}^2-k^2}} \right],$

(4.18)

with

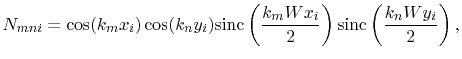$\displaystyle N_{mni}=\cos(k_{m}x_{i})\cos(k_{n}y_{i})\sinc \left(\frac{k_{m}Wx_{i}}{2}\right)\sinc \left(\frac{k_{n}Wy_{i}}{2}\right),$

(4.19)

$\displaystyle N_{mnj}=\cos(k_{m}x_{j})\cos(k_{n}y_{j})\sinc \left(\frac{k_{m}Wx_{j}}{2}\right)\sinc \left(\frac{k_{n}Wy_{j}}{2}\right),$

(4.20)

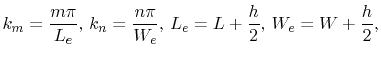$\displaystyle k_{m}=\frac{m\pi}{L_{e}},\,k_{n}=\frac{n\pi}{W_{e}},\,L_{e}=L+\frac{h}{2},\,W_{e}=W+\frac{h}{2},$

(4.21)

$\displaystyle L_{mn}=\begin{cases} 1&\text{, if $m=0\vee n=0$},\\ 2&\text{, ... ...edge (m=0\vee n\neq 0)$},\\ 4&\text{, if $m\neq 0\vee n\neq 0$}, \end{cases}$

(4.22)

and

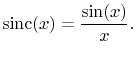$\displaystyle \sinc (x)=\frac{\sin(x)}{x}.$

(4.23)

**Figure 4.2:** Rectangular, parallel metallic planes with four open edges. Equation (4.18) contains the port impedance matrix elements.
$\includegraphics[width=13cm,viewport=130 595 500 755,clip]{{pics/Open_Edges.eps}}$

In (4.18) $k=\omega/c_{l}$ denotes the wave number, with the speed of light $c_{l}$ . $L_{e}$ and $W_{e}$ are the effective plane length and width, respectively. These effective dimensions consider the fringing fields at the cavity edges according to [45]. [43] also provides an analytical solution for equilateral triangular parallel planes with three open edges. Chapter 7 of this work presents an analytical solution for rectangular parallel planes with one open and three closed edges. This is a powerful solution for predesign investigations of the radiated emissions from the slot of a slim cubical enclosure, because discussion of the bias functions of the model provides direct information about the influence of the source position on the emission level.
The analytical method of [43] enables the calculation of parallel plane cavities with fairly arbitrary shapes by connecting rectangular or equilateral triangular parallel-plane segments. This method is illustrated in Figure 4.3.

**Figure 4.3:** Three rectangular cavities are connected together with interface ports.
$\includegraphics[width=13cm,viewport=130 630 500 755,clip]{{pics/Port_Connection.eps}}$

C. Poschalko: The Simulation of Emission from Printed Circuit Boards under a Metallic Cover

			Dissertation Christian Poschalko
Previous: 4.1.2 Summary of the cavity model equations Up: 4 Cavity model of the electromagnetic field between Next: 4.3 Inductance, capacitance, resistance (LCR) grid solution method