5.5 Link of the common mode coupling to the near field above the PCB

Near field scanning over a PCB is a state of the art method to investigate the EMC performance experimentally [81], [82]. Usually the magnetic field vector components $\vert H_{x}\vert$, $\vert H_{y}\vert$ and $H_{mag}=\sqrt{\vert H_{x}\vert^2+\vert H_{y}\vert^2}$ are scanned versus frequency as depicted in Figure 5.10. Phase information can either be obtained with a double probe time domain scanner [83], [84], or by the method of [85], which obtains the phase from two magnitude scans with different scan heights above the PCB.

Figure 5.10: Scanning the magnetic field above the PCB with a magnetic field probe.

Increased field value areas on the PCB are observed as potential electromagnetic emission sources. However, there is actually no direct relation from the scanned field values to the coupling of the PCB to a cavity field. The coupling of an IC to the cavity field inside a $\mu$TEM cell is tested with the standardized IC EMC compliant measurement of [54]. Therefore, investigations have been carried out to predict the results of these IC $\mu$TEM measurements with scanned field data and with simulations. [81] utilizes empirical formulations for a first order prediction of $\mu$TEM cell IC measurements from near field measurement data. [6] and [52] modeled the coupling from an IC to a $\mu$TEM cell with coupling capacitors. These models had some inaccuracies especially for frequencies above 300MHz and did not reveal any relationship to the near field above the IC. Only three-dimensional full wave simulations or the mulipole method of [31] enable an accurate prediction of the PCB or IC cavity coupling from near field data. However, these methods do not preserve the initial near field localization of the critical sources on the PCB.
It has previously been described that only the vertical current segments couple to the cavity. This enables a direct relation to be expressed from the scanned near field to the common mode coupling. The third Maxwell equation in air

$$\vec{\nabla}\vec{H}=\vec{J}+j\omega\epsilon_{0}\vec{E},$$ (5.13)

relates the magnetic field density $\vec{H}$ to the electric field density, $\vec{E}$ and the current density $\vec{J}$. The dielectric constant in air is $\epsilon_{0}$. Equation (5.13) is utilized to express the vertical current density

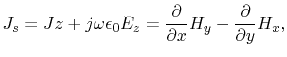$$J_{s}=J{z}+j\omega\epsilon_{0}E_{z}=\frac{\partial}{\partial x}H_{y}-\frac{\partial}{\partial y}H_{x},$$ (5.14)

which excites the cavity field. This current density can be introduced into a cavity model with the weighting factor

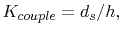$$K_{couple}=d_{s}/h,$$ (5.15)

where $d_{s}$ denotes the height of the scanning plane above the parallel ground plane. When a scan would be carried out directly on the trace, without any distance of the scan plane (theoretically), the current $J_{s}$ would become the trace current and the coupling weighting factor would become $d/h$. Equation (5.14) reveals that not the field density values, but their derivatives are significant for the common mode coupling to the cavity. Therefore, a scan plot of 5.14 will provide much more precision for coupling source identification. Figure 5.11 depicts both, $\vert H_{x}\vert$ and $\vert\partial H_{x}/\partial y\vert$, along a short trace in y-direction. The vertical segments that couple to the cavity can clearly be localized from $\vert\partial H_{x}/\partial y\vert$. $\vert H_{x}\vert$ is nearly constant along the whole horizontal trace segment which does not couple to the cavity. For maximum source localization accuracy, the scan has to be performed as close as possible along the PCB or IC surfaces and the scan heights above the PCB ground plane must be taken into account using (5.15) for the classification of the source coupling potentials.

Figure 5.11: $\vert H_{x}\vert$ and $\vert\partial H_{x}/\partial y\vert$ along the y direction. $\vert\partial H_{x}/\partial y\vert$ enables an accurate identification of the coupling current segments, while $\vert H_{x}\vert$ is high along the whole trace length.

The following subsections describe some application opportunities for  (5.14) and (5.15) beyond source identification.

Subsections

• 5.5.1 Prediction of $\mu$TEM IC measurements from near field scan data.
• 5.5.2 IC EMC model validation with near field scan data
• 5.5.3 Behavior modeling of geometrically complex components

C. Poschalko: The Simulation of Emission from Printed Circuit Boards under a Metallic Cover