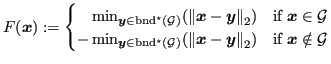Figure 2.2:
Implicit geometries
|
|
Let
 be a geometry. A function
be a geometry. A function
 with
with
 and
and
 is called the implicit representation of
is called the implicit representation of
 . The function used for this representation is not unique. However, there is a guarantee that for every geometry
. The function used for this representation is not unique. However, there is a guarantee that for every geometry
 there exists an implicit representation.
The existence of such a function
there exists an implicit representation.
The existence of such a function  for a given geometry
for a given geometry
 can easily be shown by setting
can easily be shown by setting
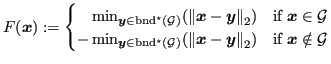 |
(2.2) |
For example, the closed  -ball with radius
-ball with radius  and center
and center  can be represented using the function
can be represented using the function
 .
Another popular example of objects represented by implicit functions are metaballs [70]. Metaballs are organic-looking ball-like objects fulfilling an implicit function which is based on distances to ball centers.
These two examples of geometries represented with implicit functions are visualized in Figure 2.2.
Implicit geometries can also be used to represent multi-region geometries with one implicit function
.
Another popular example of objects represented by implicit functions are metaballs [70]. Metaballs are organic-looking ball-like objects fulfilling an implicit function which is based on distances to ball centers.
These two examples of geometries represented with implicit functions are visualized in Figure 2.2.
Implicit geometries can also be used to represent multi-region geometries with one implicit function  for each region.
Although geometries represented by mathematical expressions are robust with respect to modeling, they rarely are used in engineering applications, because finding a function in closed form is challenging for general objects.
for each region.
Although geometries represented by mathematical expressions are robust with respect to modeling, they rarely are used in engineering applications, because finding a function in closed form is challenging for general objects.
florian
2016-11-21