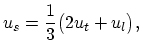2.5.2.2 Intravalley Scattering by Acoustic Phonons

This type of scattering assumes that the initial and final states of an electron are within the same valley. The acoustic scattering mechanism is assumed to be elastic which is an approximation called equipartition [18]. For this type of scattering the transition probability is given by:

$$\lambda(\epsilon)=\frac{2\pi k_{B}T_{L}D_{A_{i}}^{2}}{\hbar u_{s}^{2}\rho}g_{i}(\epsilon),$$ (2.107)

where $i$ is the valley index, $T_{L}$ is the lattice temperature, $D_{A_{i}}$ is the acoustic deformation potential of the $i$-th valley, $u_{s}$ denotes the average sound velocity, $\rho$ is the density of the crystal and $g_{i}\left(E\right)$ the density of states per spin in the $i$-th valley which is defined by the following formula:

$$g_{i}(\epsilon)=\frac{1}{(2\pi)^{3}}\int_{BZ}\delta(\epsilon-\epsilon_{i}(\vec{k}))\,d^{3}k.$$ (2.108)

For the analytical band structure (2.77) it follows from (2.108):

$$g_{i}(\epsilon)=\frac{1}{(2\pi)^{2}}\frac{2m_{d_{i}}^{*}}{\hbar^{2}}\sqrt{\gamma_{i}(\epsilon)}(1+2\alpha_{i}\epsilon),$$ (2.109)

where $m_{d_{i}}^{*}$ is the density of states effective mass for the $i$-th valley, and $\gamma_{i}\left(E\right)$ denotes the band-form function:

$$\gamma_{i}(\epsilon)=\epsilon(1+\alpha_{i}\epsilon).$$ (2.110)

The average sound velocity is defined as:

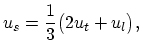$$u_{s}=\frac{1}{3}\bigl(2u_{t}+u_{l}\bigr),$$ (2.111)

where $u_{t}$ and $u_{l}$ are the transverse and longitudinal components of the sound velocity.

The numerical values for the parameters [18,20] of the acoustic phonon scattering rate are given in table Table 2.2.

Table 2.2: Numerical values for the acoustic phonon scattering rate.

	$D_{A_{X}}$	$D_{A_{L}}$	$\rho$	$u_{t}$	$u_{l}$
Silicon	7.2 eV	11.0 eV	2.338$\times$10$^{-3}$ kg/cm$^{3}$	5.410$\times$10$^{5}$ cm/sec	9.033$\times$10$^{5}$ cm/sec
Germanium	9.58 eV	8.84 eV	5.32$\times$10$^{-3}$ kg/cm$^{3}$	3.61$\times$10$^{5}$ cm/sec	5.31$\times$10$^{5}$ cm/sec

S. Smirnov: