2.5.3.2 Scattering Rate

2.5.3.2 Scattering Rate

The scattering rate due to electron-plasmon interaction can be obtained using Fermi's golden rule (2.95) and the Hamiltonian (2.130). Plasmon scattering of electrons represents the long-range part of the electron-electron interaction [39]. Assuming a nonparabolic and spherical analytical band structure (2.77), the scattering rate is given by:

$\displaystyle \lambda_{plas}\left(k\right)=\frac{e^{2}\hbar} {16\pi\varepsilon\... ...pm\frac{1}{2}\right)\left(k^{2}-k_{f}^{2}\right)^{2} \ln\frac{q_{c}}{q_{\min}},$

(2.131)

The final electron energy is given as:

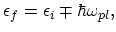$\displaystyle \epsilon_{f}=\epsilon_{i}\mp\hbar\omega_{pl},$

(2.132)

where the plasma frequency is (see Appendix B):

$\displaystyle \omega_{pl}=\sqrt{\frac{{{e^{2}}}}{{\varepsilon}}\sum_{v}\frac{n_{v}}{(m_{d}^{*})_{v}}}.$

(2.133)

Here the summation over all possible valleys is assumed, and $n_{v}$ stands for the contribution from valley

to the electron density.

The cut-off wave vector $q_{c}$ is defined as follows:

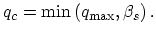$\displaystyle q_{c}=\min\left(q_{\max},\beta_{s}\right).$

(2.134)

$q_{\min}$ and $q_{\max}$ stand for the boundaries of the momentum transfer:

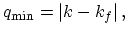		$\displaystyle q_{\min}=\left\vert k-k_{f}\right\vert,$	(2.135)
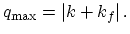		$\displaystyle q_{\max} = \left\vert k+k_{f}\right\vert.$

$k_{f}$ is the final wave vector defined by the equation:

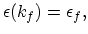$\displaystyle \epsilon(k_{f})=\epsilon_{f},$

(2.136)

$N\left(\omega_{pl}\right)$ is the average number of the plasmon excitations defined by the equilibrium Bose-Einstein statistics:

$\displaystyle N\left(\omega_{pl}\right)=\frac{1}{\exp\bigl(\frac{\hbar\omega_{pl}}{k_{B}T_{L}}\bigr)-1}.$

(2.137)

S. Smirnov: