2.5.5.1 Brooks-Herring Model

Within this model the scattering potential is given by

$$V(r)=\frac{Ze^{2}}{4\pi\varepsilon r}\exp(-\beta r),$$ (2.139)

where $\beta^{-1}$ is the screening length and $Z$ denotes the number of charge units of the impurity.

Using Fermi's golden rule (2.95) together with the nonparabolic band structure (2.77) one obtains for the total scattering rate:

$$\lambda_{BH}(\epsilon)=\frac{\sqrt{2}N_{I}Z^{2}e^{4}}{\varepsilon... ...c{1+2\alpha\epsilon}{{1+4\frac{\epsilon(1+\alpha\epsilon)}{\epsilon_{\beta}}}},$$ (2.140)

where parameter $\epsilon_{\beta}$ is defined by

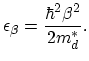$$\epsilon_{\beta}=\frac{\hbar^{2}\beta^{2}}{2m_{d}^{*}}.$$ (2.141)

The important improvements to this model are shortly described below. S. Smirnov: