3.3 Stress-Strain Relations

A mathematical expression of the stress-strain relation for the elastic deformation of materials was first suggested by Robert Hooke

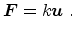$${\ensuremath{\mathitbf{F}}} = k {\ensuremath{\mathitbf{u}}}\ .$$ (3.10)

Here, ${\ensuremath{\mathitbf{F}}}$ is the applied force, ${\ensuremath{\mathitbf{u}}}$ is the deformation of the elastic body subjected to the force ${\ensuremath{\mathitbf{F}}}$, and $k$ is the material dependent spring constant. Cauchy generalized Hooke's law for three dimensional elastic bodies

$$\sigma_{ij} = C_{ijkl} \varepsilon_{kl}\ ,$$ (3.11)

where $C_{ijkl}$ is the elastic stiffness tensor of order four, which contains 81 entries. The number of components can be reduced invoking symmetry arguments [Kittel96]. For a cubic semiconductor such as Si, Ge or GaAs, there are only three independent components, namely $c_{11}, c_{12}$, and $c_{44}$. The elastic stiffness constants for Si and Ge are given in Table 3.1.

Table 3.1: Elastic stiffness constants of Si and Ge [Levinshtein99].

	Silicon	Germanium	Units
$c_{11}$	166.0	126.0	GPa
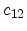$c_{12}$	64.0	44.0	GPa
$c_{44}$	79.6	67.7	GPa

Exploiting the symmetry of a cubic semiconductor the elastic stiffness tensor can be written as a $6\times 6$ matrix, and generalized Hooke's law reduces to a set of six equations

$$\begin{pmatrix}\sigma_{xx} \\ \sigma_{yy} \\ \sigma_{zz} \\ \sigm... ...remath{\varepsilon_{xz}}} \\ 2{\ensuremath{\varepsilon_{xy}}} \\ \end{pmatrix}.$$ (3.12)

If the stresses are known, the values for the strains are to be determined by inversion of (3.11). Introducing the elastic compliance tensor $S_{ijkl}$, the inverted equation becomes in the index notation

$$\varepsilon_{ij} = S_{ijkl} \sigma_{kl}\ ,$$ (3.13)

or in matrix form

$$\begin{pmatrix}{\ensuremath{\varepsilon_{xx}}} \\ {\ensuremath{\v... ...} \\ \sigma_{zz} \\ \sigma_{yz} \\ \sigma_{xz} \\ \sigma_{xy} \\ \end{pmatrix}.$$ (3.14)

The elastic compliance constants $s_{ij}$ are related to the elastic stiffness constants $c_{ij}$ via

$$s_{11} = \frac{c_{11}+c_{12}}{c_{11}^2 + c_{11} c_{12} - 2 c_{12}^2}\ ,$$

$$s_{12} = \frac{-c_{12}}{c_{11}^2 + c_{11} c_{12} - 2 c_{12}^2}\ ,\quad\mathrm{and}$$

$$s_{44} = \frac{1}{c_{44}}\ .$$

Note that the stiffness constants are traditionally represented by the symbol $c_{ij}$, while $s_{ij}$ is reserved for the compliance constants.

Subsections

• 3.3.1 The Miller Index Notation
• 3.3.2 Strain Resulting from Uniaxial Stress
• 3.3.3 Strain Resulting from Epitaxy

E. Ungersboeck: Advanced Modelling Aspects of Modern Strained CMOS Technology