3.5.3 $D_{4h}$ symmetry

If stress is applied along a fourfold axis ${\ensuremath{\mathitbf{e}}}_i$ of a cubic lattice of symmetry class $O_h$, the unit cube becomes a square cuboid (rectangular parallelepiped on a square base), representing the Bravais parallelepiped belonging to symmetry class $D_{4h}$ [Bir74]. Note, that $D_{4h}$ is a member of the tetragonal crystal system. A similar symmetry reduction is observed, if biaxial strain is present in a {001} plane. According to Table 3.2 the point group $D_{4h}$ has 16 symmetry elements, since only one fourfold axis and no threefold axis remains.

The strain tensor in the principal system yielding a $O_h \rightarrow D_{4h}$ symmetry reduction has non-zero elements in the diagonal (e.g. ${\ensuremath{\varepsilon_{11}}} = {\ensuremath{\varepsilon_{22}}} \neq {\ensuremath{\varepsilon_{33}}}$), whereas all off-diagonal elements vanish.

Figure 3.8: Irreducible wedge of the first BZ of a diamond structure stressed along direction [100].

The symmetry operations yield invariance of the energy bands under reflections

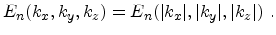$$E_{n}(k_{x},k_{y},k_{z}) = E_{n}(\vert k_{x}\vert,\vert k_{y}\vert,\vert k_{z}\vert)\ .$$ (3.39)

and the invariance of the energy bands under the permutation of the indices perpendicular to the direction of stress. If stress is applied along [100], the energy bands are invariant under the permutation

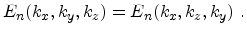$$E_{n}(k_{x},k_{y},k_{z}) = E_{n}(k_{x},k_{z},k_{y})\ .$$ (3.40)

From (3.39) it follows that the bands have to be calculated only in the first octant of the BZ. The additional symmetry of (3.40) can be exploited to further reduce the volume of the irreducible wedge by a factor of two. For band structure calculation a volume for the irreducible wedge can be chosen which combines three irreducible wedges of the relaxed crystal in the limit of vanishing strain. These wedges are depicted in Figure 3.8. They are labeled with a number and can be transformed into the first irreducible wedge of the relaxed crystal by a symmetry operation

$$\ensuremath{{\underaccent{\bar}{T}}}_1 = \begin{pmatrix}1 & 0 & 0... ...t{\bar}{T}}}_3 = \begin{pmatrix}0 & 1 & 0\\ 0 & 0 & 1\\ 1 & 0 & 0\end{pmatrix}.$$ (3.41)

The volume of the irreducible wedge depicted in Figure 3.8 is $\Omega_\mathrm{BZ}/16$ and thus complies with relation (3.34).

E. Ungersboeck: Advanced Modelling Aspects of Modern Strained CMOS Technology