Energy Dispersion of the Conduction Band Minimum of Strained Si: Method 1

The effect of strain on the spectrum near the lowest conduction band edge is estimated by expanding the root in (3.73) and neglecting terms proportional to ${\ensuremath{\varepsilon_{}}}^2$ and $k^4$. The spectrum is expanded near the minimum of the conduction band $\Delta _1$ at ${\ensuremath{\mathitbf{k}}}_{\mathrm{min}} = 2\pi / a_0 (0,0,0.85)$ of the unstrained lattice.

$$E(\hat{{\ensuremath{\varepsilon_{}}}},{\ensuremath{\mathitbf{k}}}... ...rac{2 \Xi_{u'}A_3{\ensuremath{\varepsilon_{xy}}}}{\vert A_4\vert k_0}k_x k_y\ .$$ (3.76)

By comparing this equation with (3.28) the constants $A_1$ and $A_2$ are given by

$$A_1 = \frac{\hbar^2}{2 \ensuremath{m_\mathrm{l}}}\ ,$$ (3.77)

$$A_2 = \frac{\hbar^2}{2 \ensuremath{m_\mathrm{t}}}\ ,$$ (3.78)

which leaves only $A_3$ undetermined.

At zero shear strain, the splitting between the two lowest conduction bands, which is denoted as $\Delta$ (see (3.74)), can be related to $A_4$ by evaluating (3.73) at ${\ensuremath{\mathitbf{k}}} = {\ensuremath{\mathitbf{k}}}_{\mathrm{min}}$

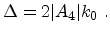$$\Delta = 2 \vert A_4\vert k_0\ .$$ (3.79)

Thus, the last term of (3.76) can be written as

$$\frac{4 A_3 \Xi_{u'}}{\Delta}{\ensuremath{\varepsilon_{xy}}}k_xk_y\ .$$ (3.80)

Since this term is proportional to ${\ensuremath {\varepsilon _{xy}}}$ and $k_xk_y$, it describes a change in effective mass proportional to strain. A kp theory capable of describing the change in the effective mass due to strain must contain third order terms proportional to $\hat{{\ensuremath{\varepsilon_{}}}}k^2$. It was shown by Bir and Pikus [Bir74] that the dominating $\hat{{\ensuremath{\varepsilon_{}}}}k^2$ correction to the spectrum $E(\hat{{\ensuremath{\varepsilon_{}}}},{\ensuremath{\mathitbf{k}}})$ of the lowest conduction band at ${\ensuremath{\mathitbf{k}}}_{\mathrm{min}}$ is

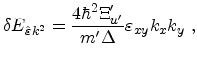$$\delta E_{\hat{{\ensuremath{\varepsilon_{}}}}k^2} = \frac{4 \hbar^2 \Xi'_{u'}}{m' \Delta}{\ensuremath{\varepsilon_{xy}}} k_x k_y\ ,$$ (3.81)

where

$$\frac{1}{m'} = \frac{2}{\ensuremath{\mathrm{m}}_0^2} \sum_{n\neq ... ...vert n\rangle \langle n\vert p_y \vert\Delta_{2'}\rangle }{E_n-E_{\Delta_1}}\ ,$$ (3.82)

and $\Xi'_{u'}$ denotes the deformation potential constant $\Xi _{u'}$ evaluated at ${\ensuremath{\mathitbf{k}}}_{\mathrm{min}}$.

The coefficient $A_3$ can now be obtained by comparing (3.80) with (3.81). Assuming that the deformation potential constant $\Xi _{u'}$ is the same at both points $X$ and ${\ensuremath{\mathitbf{k}}}_{\mathrm{min}}$, that is $\Xi_{u'}= \Xi'_{u'}$, $A_3$ is given by

$$A_3 = \frac{\hbar^2}{m'}\ ,$$ (3.83)

and the energy dispersion (3.76) around the conduction band edge becomes

$$E(\hat{{\ensuremath{\varepsilon_{}}}},{\ensuremath{\mathitbf{k}}}... ... - \frac{4 \hbar^2 \Xi_{u'}{\ensuremath{\varepsilon_{xy}}}}{m'\Delta}k_x k_y\ .$$ (3.84)

Here, the diagonal entries of the strain tensor were assumed to be zero, since they do not cause a change in the effective mass in this approximation. The impact of shear strain $\varepsilon_{xy}$ on the effective masses becomes clearer when changing the coordinate system

$$x' \rightarrow [110] \qquad y' \rightarrow [1\bar{1}0] \qquad z' \rightarrow [001]\ .$$

This coordinate system is rotated 45$^\circ$ about the $z$ axis with respect to the principal coordinate system, thus,

$$k_{x'} = \frac{k_x+k_y}{\sqrt{2}} \qquad k_{y'} = \frac{k_x-k_y}{\sqrt{2}} \qquad k_{z'} = k_{z}\ .$$ (3.85)

In the rotated coordinate system the effective mass tensor is diagonal

$$E(\hat{{\ensuremath{\varepsilon_{}}}},{\ensuremath{\mathitbf{k}}}') = \frac{\hbar^2 (k_{z'} - k_\mathrm{min})^2}{2 \ensuremath{m_\mat... ...u'} \ensuremath{m_\mathrm{t}}}{m'\Delta}{\ensuremath{\varepsilon_{xy}}}\right )$$

$$= \frac{\hbar^2 (k_{z'} - k_\mathrm{min})^2}{2 \ensuremath{m_\mat... ...frac{\hbar^2 k_{y'}^2}{2 m_{\mathrm{t},y'}({\ensuremath{\varepsilon_{xy}}})}\ .$$ (3.86)

Two transverse masses occur

$$m_{\mathrm{t},x'} = \ensuremath{m_\mathrm{t}}(1 + \eta \kappa {\ensuremath{\varepsilon_{xy}}})^{-1}\ ,$$ (3.87)

$$m_{\mathrm{t},y'} = \ensuremath{m_\mathrm{t}}(1 - \eta \kappa {\ensuremath{\varepsilon_{xy}}})^{-1}\ ,$$ (3.88)

that depend strain. Here, two parameters

$$\kappa = 4 \Xi_{u'}/\Delta \quad\mathrm{and}\quad \eta = \ensuremath{m_\mathrm{t}}/(2 m')$$ (3.89)

have been introduced.

Within this approximation the effect of shear strain on the transverse masses of Si can be modeled. It was developed by Bir and Pikus [Bir74] and Hensel [Hensel65]. In the following, a more rigorous model is presented, which is also able to predict the effect of shear strain on the longitudinal mass, the splitting between conduction band valleys, and the change of position of the conduction band minimum.

E. Ungersboeck: Advanced Modelling Aspects of Modern Strained CMOS Technology