4.3.1 Band Gap Energy

The Varshni formula [313] well describes the temperature dependence of the band gap in nitrides with:

$$\ensuremath{\ensuremath{\mathcal{E}}_{\ensuremath{\mathrm{g}}}}=E... ...remath{\mathrm{g}} T_\mathrm{L}^2}{\beta_\ensuremath{\mathrm{g}}+T_\mathrm{L}}.$$

The values for $E_\ensuremath{\mathrm{g,0}}$ (energy band gap at 0 K), $\alpha_\ensuremath{\mathrm{g}}$, and $\beta_\ensuremath{\mathrm{g}}$ (empirical constants) for GaN, AlN and InN are summarized in Table 4.6. The parameters for GaN are an average of various reported results as summarized in [209], those for AlN are based on the experimental work of Guo et al. [314]. For InN the parameters are taken from [315], where three different techniques were used to study the band gap energy and its properties. The results are in agreement with the recently reevaluated band gap energy of InN as discussed in Section 3.3.

Table 4.6: Summary of band structure model parameters.

Material	E $_\ensuremath{\mathrm{g,0}}$ [eV]	$\alpha_\ensuremath{\mathrm{g}}$ [eV/K]	$\beta_\ensuremath{\mathrm{g}}$ [K]
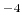GaN	3.4	9.09$\times$10$^{-4}$	800
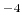AlN	6.2	18.0$\times$10$^{-4}$	1462
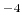InN	0.69	4.14$\times$10$^{-4}$	454

The band gap of semiconductor alloys is interpolated by Vegard's law [316]:

$$\ensuremath{\ensuremath{\mathcal{E}}_{\ensuremath{\mathrm{g}}}}^\... ...remath{\mathrm{g}}}}^\ensuremath{\mathrm{BC}}x+C_\ensuremath{\mathrm{g}}(1-x)x,$$

with the bowing parameter $C_\ensuremath{\mathrm{g}}$. The reported values for Al$_x$Ga$_{1-x}$N of the latter show a large variation ranging from $-$0.8 eV [317] to $+$1.33 eV [318]. However, several experiments [319,320] show a linear variation ( $C_\ensuremath{\mathrm{g}}\approx$0 eV) which is adopted here.

For InGaN a bowing parameter $C_\ensuremath{\mathrm{g}}$=1.4 eV in agreement with the work of Walukievicz et al. [315] is well established. It corresponds to the theoretical value given by Caetano et al. [321] ( $C_\ensuremath{\mathrm{g}}$=1.44 eV). Other theoretical studies show that a single bowing parameter cannot be used for the whole alloy band gap [322,323]. While the dependence of the bowing parameter on the composition in the aforementioned works is weak, it still remains to be experimentally verified. Until such studies are available, $C_\ensuremath{\mathrm{g}}$=1.4 eV and $C_\ensuremath{\mathrm{g}}$=2.1 eV for unstrained and strained samples, respectively, are adopted [324]

Several works suggest a bowing parameter with a value ranging from 3.0 eV and 6.1 eV [315,325] for InAlN. Those large disagreements can be attributed to low crystalline quality and high doping levels. Recent calculations and experimental studies showed, however, that the bowing parameter for InAlN is strongly dependent on the material composition [326,327]. In order to account for this dependence the following expression is proposed in [327]:

$$C_\ensuremath{\mathrm{g}}(x) = \frac{C_{\ensuremath{\mathrm{g}},1}}{1+C_{\ensuremath{\mathrm{g}},2} x}.$$

In the same work, the authors propose a value of 15.3 eV and 4.81 eV for $C_{\ensuremath{\mathrm{g}},1}$ and $C_{\ensuremath{\mathrm{g}},2}$, respectively. As shown in Fig. 4.8 this model achieves a very good agreement with the experimental data from various other studies [328,329,330]. The dependence of the band gap on composition should be attributed to charge transfer effects, related to the large electronegativity differences between III-V atoms [322]. However, as pointed out in [331] Vegard's law is applicable for lattice matched composition ($\approx$17% as reported in [332]), which is mostly interesting for HEMT applications. For reference the result obtained using a constant $C_\ensuremath{\mathrm{g}}$=3 eV is depicted, too.

Figure 4.8: Material composition dependence of the band gap of In$_x$Al$_{1-x}$N.