C. Estimating the Total Charge in the Diffusive Layer

The Poisson-Boltzmann equation can be solved for the total charge in the diffusive layer in a similar manner the way it is done for the semiconductor surface potential. Beginning with (5.13):

$$\frac{d^{2}\psi}{dz^{2}}=\frac{2\,q\,c_{0}}{\varepsilon_{0}\varepsilon_{sol}} \,\sinh\left(\frac{q \psi}{k_{\text{B}} T}\right)\quad.$$ (7.21)

Reexpressing it via the Debye length,

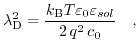$$\lambda_{\mathrm{D}}^{2}=\frac{k_{\text{B}} T\varepsilon_{0}\varepsilon_{sol}}{2\,q^{2}\,c_{0}}\quad,$$ (7.22)

leads to the following expression:

$$\frac{d^{2}\psi}{dz^{2}}=\frac{k_{\text{B}} T}{q\,\lambda_{\mathrm{D}}^{2}}\,\sinh\left(\frac{q \psi}{k_{\text{B}} T}\right)\quad.$$ (7.23)

This equation can be rewritten by applying the following identity:

$$2\frac{d\psi^{2}}{dz^{2}}\,\frac{d\psi}{dz}=\frac{d\phantom{z}}{dz}\left(\frac{d\psi}{dz}\right)^{2}\quad.$$ (7.24)

Substituting (7.24) into (7.23) leads to a first order differential euqation:

$$\begin{array}{ccc} \frac{d^{2}\psi}{dz^{2}}&=&\:\frac{1}{2}\,... ...si'\,\sinh\left(\frac{q\psi}{k_{\text{B}} T}\right) \end{array}$$ (7.25)

(7.25) can be solved via separation of variables. Under the condition of a vanishing electric field for $z\rightarrow\infty$ the following solution can be derived:

$$\begin{array}{ccl} \left(\psi'\right)^{2}&=&\,\frac{2\,k_{\te... ...ft(\frac{q\psi_{0}}{k_{\text{B}} T}\right)-1\right) \end{array}$$ (7.26)

Exploiting the identity $2\sinh^{2}\left(x/2\right)=\cosh(x)-1$, the expression for $\left(\psi'\right)^{2}$ can be formulated as:

$$\begin{array}{ccc} \left(\psi'_{0}\right)^{2}&=&\frac{4(k_{\t... ...0}}{k_{\text{B}} T}\right)}{\lambda_{\mathrm{D}} q} \end{array}$$ (7.27)

In the last calculation step Gauß's law is utilized to express the total charge per unit area in the Gouy-Chapman layer:

$$\sigma_{0}=-\varepsilon_{0}\varepsilon_{sol} \psi'_{0}=\mp\sqrt{8... ...\text{B}} Tc_{0}}\,\sinh\left(\frac{q\psi_{0}}{2\,k_{\text{B}} T}\right)\quad .$$ (7.28)