Mihail Nedjalkov MSc PhD D.Sc., Senior Postdoc Publications

Biography D.Sc. Dr. Mihail Nedjalkov, born in Sofia, Bulgaria received the Master degree in semiconductor physics at the Sofia University "Kl. Ohridski", a Ph.D. (Dr.) degree in Physics (1990), Habilitation (2001) and Doctor of Science (D.Sc.) degree in Mathematics (2011) at the Bulgarian Academy of Sciences (BAS). He is Associate Professor with the Institute of Information and Communication Technologies, BAS. He held visiting research positions at the University of Modena (1994), University of Frankfurt (1998), Arizona State University (2004) and mainly at the Institute for Microelectronics, TU Wien, supported by the following European and Austrian projects: EC Project NANOTCAD (2000-03),"Österreichische Forschungsgemeinschaft MOEL 239 and 173 (2007-08), FWF (Austrian Science Fund) P13333-TEC (1998-99), P21685-N22 (2010-2014), P27214-N27(2017- date), START (2005-06), P-21685 (2009-2014), EC-FP7 Project SUPERTHEME and the current H2020 Project SUPERAID7. He has served as a lecturer at the 2004 International School of Physics 'Enrico Fermi', Varenna, Italy, and has over 200 publications as a first or second author, among them one book and 35 book contributions. His research interests include physics and modeling of classical and quantum carrier transport in semiconductor materials, devices and nanostructures, collective phenomena, theory and application of stochastic methods.

The Wigner formulation of quantum mechanics in phase space has been initially developed on top of the Von Neumann equation with the help of the Weyl transform. It comprises a center of mass transform followed by a Fourier integral on the relative coordinate introducing the momentum variable. The latter is continuous if the limits of the integral are plus and minus infinity. Then we say that the coherence length is infinity. In the electrostatic limit, according to the Maxwell equations, the electromagnetic media is represented by the electric field only — the magnetic field vanishes. In this case, the kinetic momentum and the canonical momentum coincide. However, in the presence of a magnetic field, the two quantities differ by the vector potential.

The involvement of the magnetic field enormously complicates the theory, which, moreover, becomes dependent on the choice of the gauge — or, equivalently, the set of scalar and vector potentials. A change of the gauge does not affect the involved physics, but changes the mathematical structure — hence, the numerical implementation of the formalism. In particular, the standard electrostatic Wigner formalism is developed under the choice of a zero vector potential. A gauge-invariant quantum theory can be derived with the help of the Weyl-Stratonovich transform. The latter gives rise to a Wigner equation formulated in terms of position, kinetic momentum, and electromagnetic fields, which are physical (gauge-invariant) quantities. This result paves the way for development of general numerical approaches.

Modern nanoelectronic elements are bounded quantum systems, and thus can be associated with a finite coherence length. Accordingly, the momentum space becomes discrete. We derive the semi-discrete Wigner equation for general EM fields. For homogeneous magnetic fields, certain integrals representing the terms of the equation vanish, and the equation reduces to the discrete version of the ballistic Boltzmann equation. Then we analyze the important case of linear fields and show that these integrals can be solved analytically. In the long coherence length limit, the momentum becomes continuous, and the equation involves mixed derivatives of the Wigner function on position and momentum. This suggests a way to treat the finite coherence length case by using a finite difference approximation of these derivatives. The equation is then reformulated as a Fredholm integral equation of a second kind, which is the basis for development of stochastic numerical approaches.

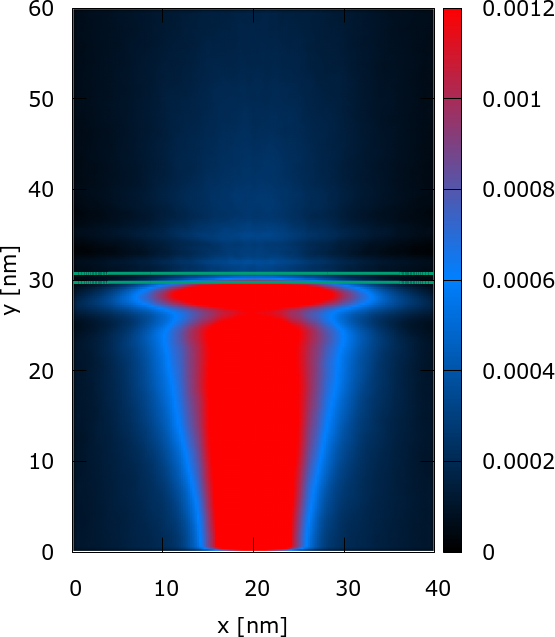
Fig. 1: Tunneling of an electron represented by a minimum uncertainty Gaussian state, evolving in the vertical direction with a kinetic energy of 0.1eV. The 0.3eV high, 1nm thick barrier, denoted by the green lines, is homogeneous along the x direction. The fine structure of the density of the tunneled part of the state is well-pronounced in the upper half (y>30nm) of the simulation domain.

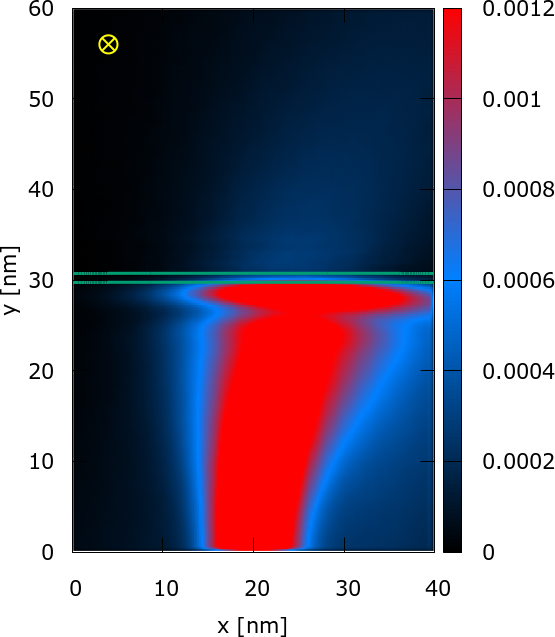
Fig. 2: Magnetotunneling: The magnetic field of -6T bends the electron density, thus destroying the symmetry of the physical task, but also destroys the fine structure in the upper half of the domain. It can be shown that the magnetic field plays a role of a decoherence factor during the electron evolution.