 |
|
Biography
Johann Cervenka was born in Schwarzach, Austria, in 1968. He studied electrical engineering at the Technische Universität Wien, where he received the degree of Diplomingenieur in 1999. He then joined the Institute for Microelectronics at the Technische Universität Wien and received his PhD degree in 2004. His scientific interests include three-dimensional mesh generation, as well as algorithms and data structures in computational geometry.
Expansion of the Deterministic Wigner Module
Carrier transport processes in nano-electronic devices require the consideration of quantum mechanics. A convenient phase-space description of quantum theory is provided by the Wigner formulation. Accordingly, several Wigner modules are being developed at the institute, and the deterministic Wigner module is being expanded by two different parallelization techniques.
The developed deterministic approach is based on the integral formulation of the Wigner equation. The overall transport process is described by separate evolutions of fundamental wave packets. Additionally, to overcome the limitations in simulation time, parallelization is required.
The first method uses the fact that the wave packets are independent. Each wave package is independently simulated from start-time to end-time and each simulation is distributed over multiple computing nodes. This method is characterized by extreme scalability, as no communication between the compute nodes is needed during simulation. Furthermore, the memory demands can be divided amongst the nodes. At the end, all partial results are combined to yield the final distribution. This method is feasible, however, only when there is no scattering during propagation, and the Wigner potential does not depend on the time evolution of other nodes.
For more complex set-ups, it is necessary to fall back on the conventional method, simulating one time-step after the other. In this case, the entire phase-space information of each wave packet has to be stored. With some consideration of the requirements, however, it is possible to simplify the simulation procedure. With respect to memory usage, it is possible to achieve an improvement by an order of magnitude.
With this second method, the different partial events are also simulated in parallel. But after each time-step the results are collected on a master node. Afterwards, updated information may be calculated, transported to the computing nodes and then the simulation of the next time-step can be triggered. In this setup, a communication overhead and synchronization between the tasks has to be taken into account.
Thanks to this extension, more complex applications can be investigated. The effects of elementary moving particles' influence on the applied potential setup can be investigated in future.
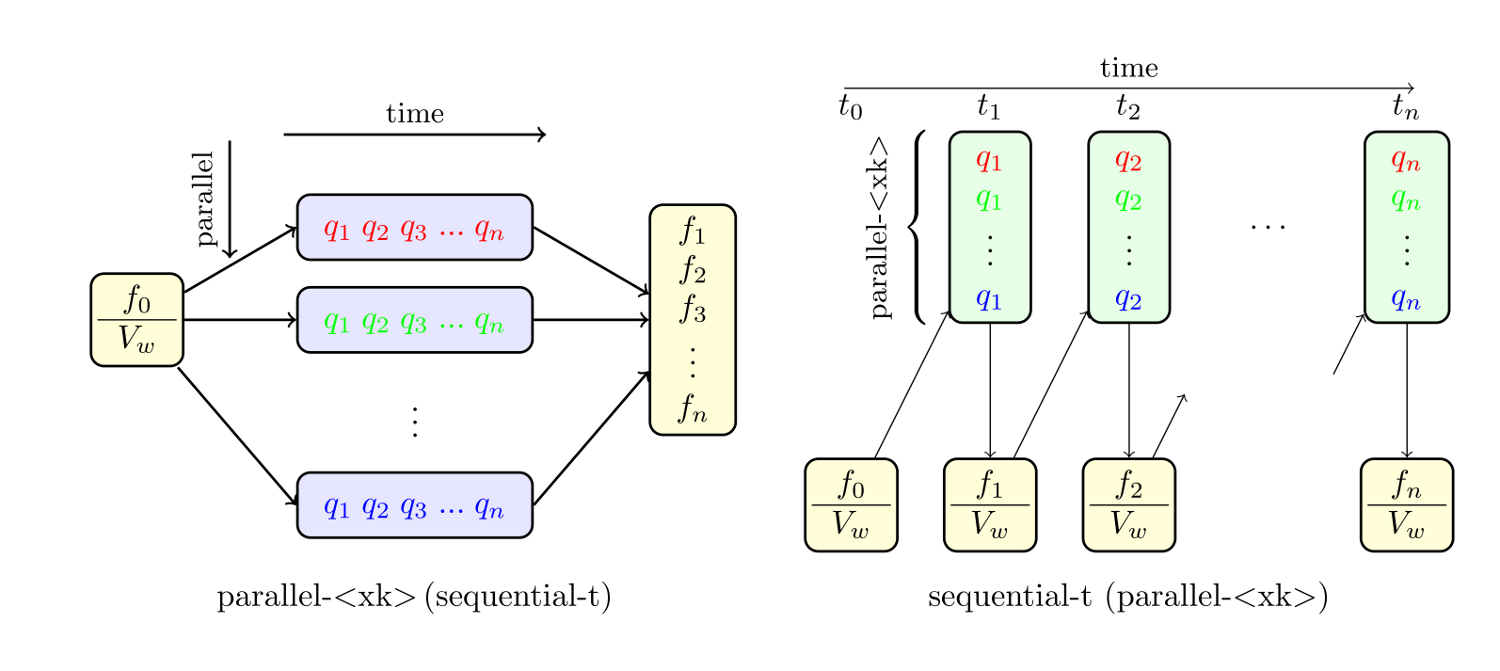
Fig. 1: Two developed simulation modes for the deterministic Wigner module.



