Andreas Morhammer Dipl.-Ing. Worked for the IμE until May 20, 2016 Publications

Microelectronic device simulation typically requires solving a set of partial differential equations on a mesh that captures the device's geometry. A posteriori error estimators provide a measure of the quality of numerical solutions obtained from such simulations by estimating the deviation (or error) of the computed solution to the exact solution. Without error estimation, one must usually resort to uniform mesh refinement, which is inefficient in terms of error reduction per additional cell, and also requires running the simulation until obtained solutions do not differ significantly from one iteration to the next, which may take significantly longer than would otherwise be necessary.
For the sake of practicality, a posteriori error estimators have to be both reliable and efficient. This means that they must neither underestimate, nor overestimate the true error by more than some fixed factor. Such error estimators are typically used for two distinct purposes: First, they allow one to judge whether an obtained solution is within the acceptable error tolerance or whether another iteration with increased resolution is necessary; second, they often provide a measure of the local error and can thus be used to identify regions where an increase in mesh resolution will be most effective in reducing the overall error, thereby providing the means for steering local mesh refinement.
We implemented an edge-based residual error estimator for 2D P1 finite elements that is both reliable and efficient for elliptic partial differential equations. Fig. 1 shows an exemplary solution computed using our implementation of the finite element method and said error estimator. We then adapted this error estimator to the finite volume method and empirically tested its behavior for drift-diffusion (DD) equations, since a comprehensive convergence theory is still lacking for such problems. Results (see for example Fig. 2) of a DD-simulation of a MOSFET with a very rough initial mesh show correct qualitative behavior, i.e. the refinement is primarily focused on the channel, as well as good speeds of convergence for the electric current, compared to solutions derived from a uniform refinement process.

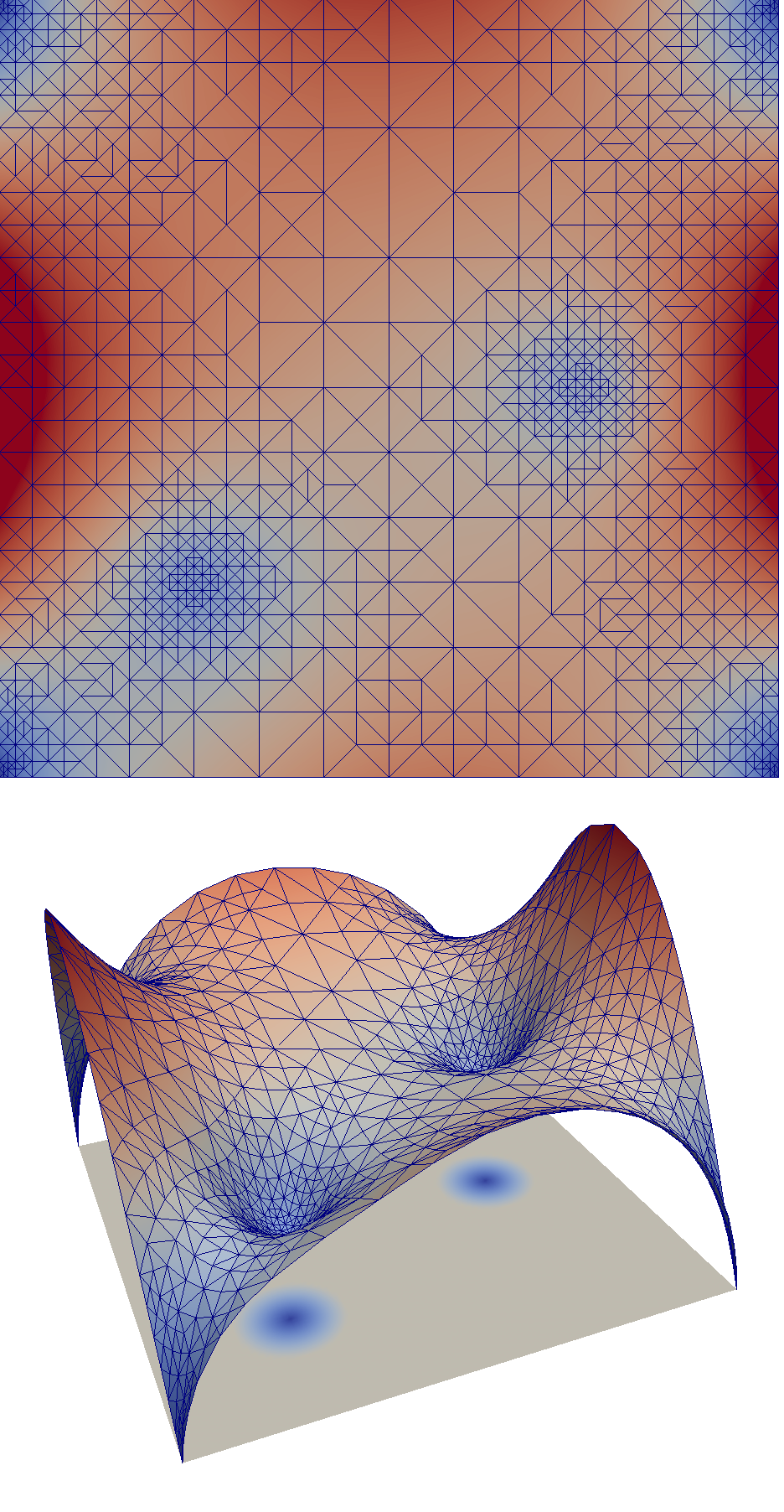
Fig. 1: Visualizations of a finite element solution and its refined mesh after nineteen iterations using our edge-based error estimator. The solved Possion problem is specified on a quadratic domain with sinusoidal Dirichlet boundary conditions at the left and right sides and sinusoidal Neumann boundary conditions at the top and the bottom. The two blue spots in the second figure represent sinks, i.e. areas where the right-hand side of Poisson's equation is negative. In the remaining grey area the right-hand side vanishes. One can observe that the error estimator, and hence mesh refinement, focuses on areas where the gradient changes a lot, such as at the singularities in the corners or near the sinks, while leaving the mesh fairly coarse in places where the solution exhibits smooth behavior.

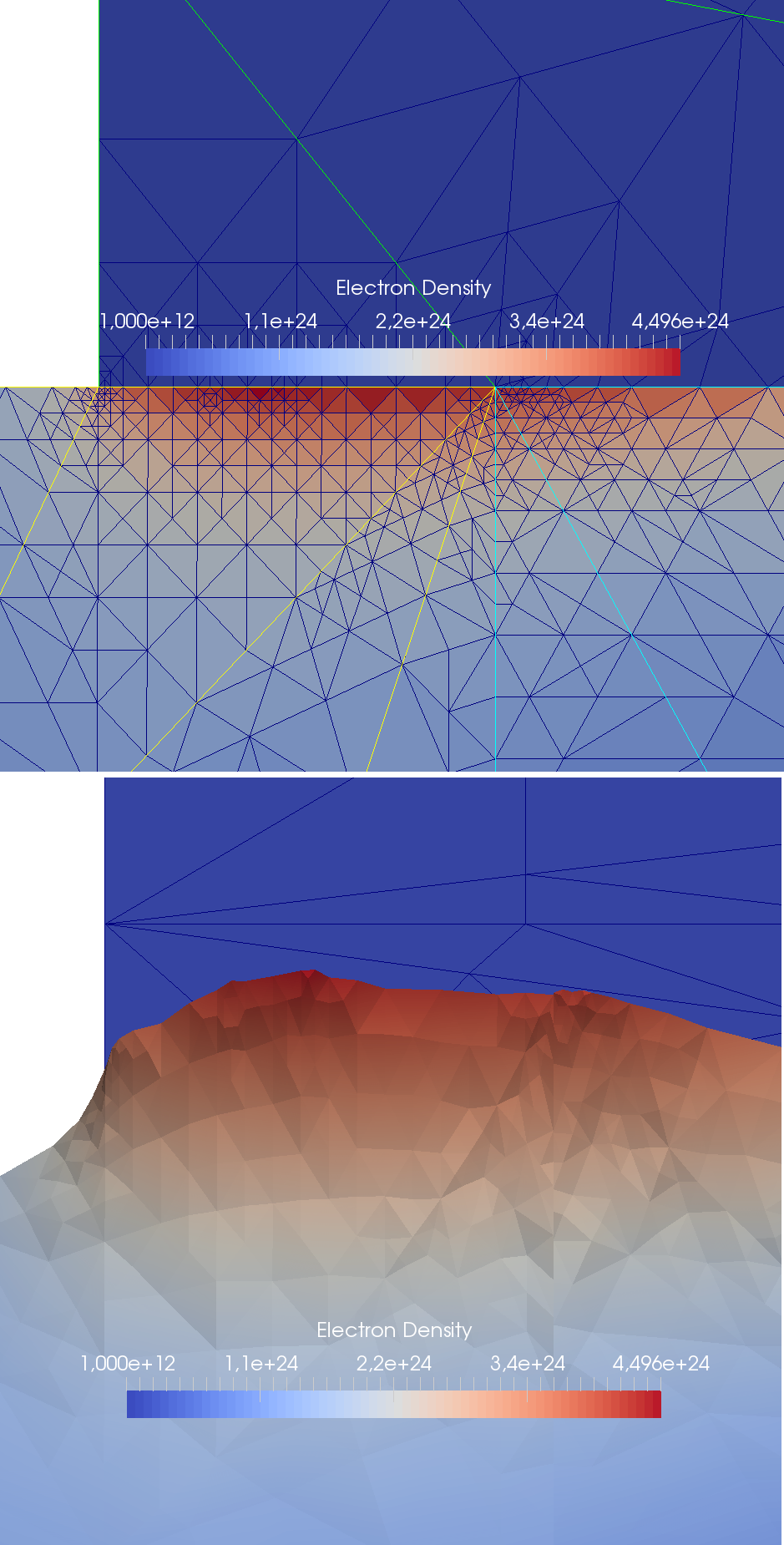
Fig. 2: Visualizations of the electronic density in charges per m³ of a DD simulation of an nMOSFET at the channel. The yellow, turquoise, and green edges in the first figure represent the initial mesh of the drain, body, and oxide region, respectively. One can observe that the error estimator, and hence mesh refinement, focuses on the channel.