Markus Kampl Dipl.-Ing. Dr.techn. Publications

Over the past few years, we have implemented a stable backward Monte Carlo method and developed a physical model for electron-electron scattering. It is commonly accepted that electron-electron scattering alters the high-energy tail of the distribution function. We have observed that in order to avoid numerical artifacts in the distribution function, one has to deal carefully with energy conservation. Simultaneous conservation of energy and momentum can be satisfied most straightforwardly with a parabolic band model. For a full band structure, however, a numerical search of the final state has to be performed. Our model assumes that the hot electrons from the channel interact with the cold electrons in the drain region. This model also predicts a Maxwellian high-energy tail of the distribution function in the presence of electron-electron scattering. An alteration of the high-energy tail can be expected only if the partner electrons are in non-equilibrium. Fig. 1 shows how electron-electron scattering enhances the energy relaxation of the channel's hot electrons in the drain region. The simulation has been carried out for parabolic bands to allow for exact energy and momentum conservation.

Another improvement in regards to the Vienna Monte Carlo simulator and the backward Monte Carlo method has been a reduction in statistical error due to symmetric particle injection. The distribution of the initial states of the backward trajectories can be chosen freely. The chosen distributions, such as a Maxwellian or a velocity weighted Maxwellian, are in general symmetric. Wave vectors generated randomly from this distribution however will have a non-zero mean value due to the finite sample size. A zero mean value can be enforced by generating the wave vectors always in pairs with opposite signs. In this way, one source of statistical error can be eliminated. The symmetric current estimator always shows less statistical error than the non-symmetric one. Furthermore, the symmetric current estimator will give zero current in thermal equilibrium without statistical error and gives reduced statistical error in situations close to thermal equilibrium.

In January, I joined the Christian Doppler Laboratory for single defect spectroscopy, where I am working on the measurement and characterization of single defects in silicon carbide.

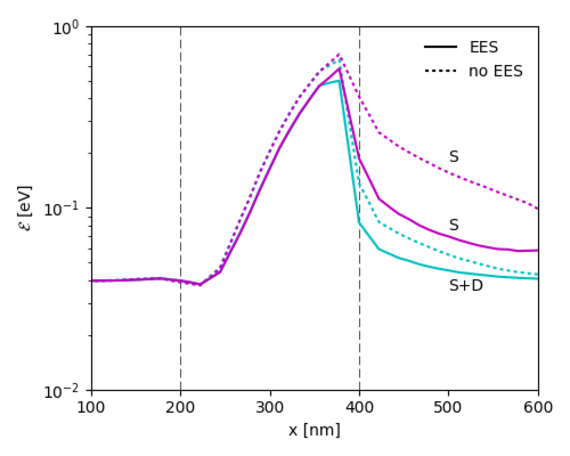
Fig. 1: Average electron energy in an n⁺n^-n⁺ diode. The upper curves (S) consider only the (hot) electrons originating from the source region and clearly show the additional energy relaxation due to electron-electron scattering. The lower curves (S+D) consider all electrons and show a stronger carrier cooling because in addition to energy relaxation, there also occurs a mixing of the hot carriers with the cold carriers in the drain.