 |
|
Biography
Michael Quell was born in 1993 in Vienna, Austria. He received his Bachelor's degree and the degree of Diplomingenieur in Technical Mathematics from the Technische Universität Wien in 2016 and 2018, respectively. After finishing his studies he joined the Institute for Microelectronics in June 2018, where he is currently working on his doctoral degree. He is researching high performance algorithms and data structures within the scope of the Christian Doppler Laboratory for High Performance TCAD.
Parallelized Construction of Extension Velocities for the Level-Set Method
The level-set method is widely used in different fields of science, such as computer graphics, fluid dynamics and microelectronics, to track interfaces driven by a velocity field. In the level-set method, an interface, Γ, is implicitly represented as the zero-level-set of a higher-dimensional function, namely the level-set function, φ.
In many applications, the underlying model defines the velocity field only at the interface itself. For these applications, an extension of the velocity field to (parts of) the simulation domain is required. This extension has to be performed at each time step of a simulation in order to account for the time-dependent velocity values at the interface. Therefore, the velocity extension is critical to overall computational performance.
An accelerated and parallelized approach has been developed to overcome the computational bottlenecks of the most common and serial-in-nature fast marching method. This was done through the utilization of a heap that keeps track of the computational order of the grid points. In this new approach, the level-set function itself is used to predetermine the computational order for the velocity extension. This allows one to employ alternative data structures to keep track of the computational order, such as a stack or a queue. Though, investigations have shown that using a queue yields the shortest runtimes.
The result is a straightforward parallelizable approach with reduced complexity for insertion and removal, as well as improved cache efficiency. In Fig. 1, the initial test geometry is shown, as well as how the interface evolves over time. Compared to the common fast marching method, our approach results in a serial speedup of at least 1.6 and a shared-memory parallel efficiency of 66% for 8 threads. The runtime reduction through parallelization is shown in Fig. 2 for the different data structures tested and two different spatial resolutions, and in Fig. 3, the corresponding parallel speedup is given. The reduction in the speedup for more than 8 threads is due to non-uniform memory access issues.
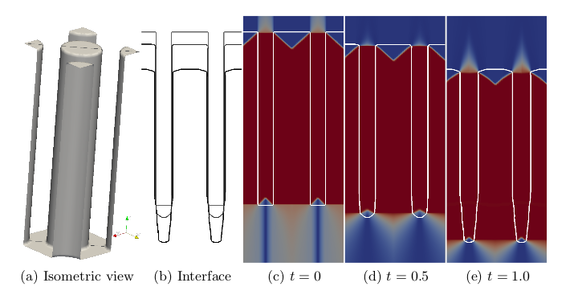
Fig. 1: (a) Initial interface in isometric view. (b)-(e) Cross-section of the simulation domain through a plane with normal (1, 1, 0): (b) Interface overlaid at different simulation times, and (c)-(e) extended velocity (low velocity in red and high in blue) for times t = 0, t = 0.5, t = 1.0.
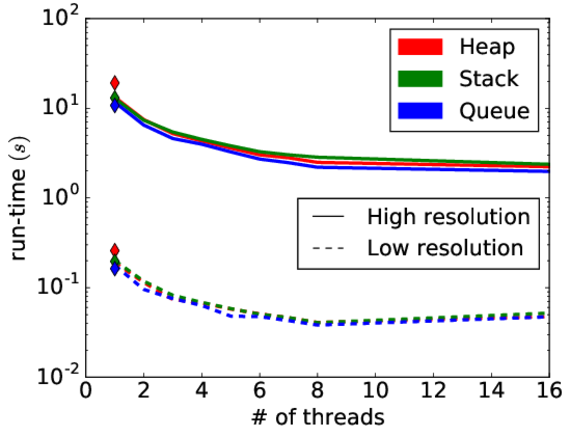
Fig. 2: Parallel runtime for the proposed parallel algorithm using a heap, stack and queue for the geometry shown in Fig. 1. For comparison, the diamonds
show the serial runtime of the improved serial algorithm (1.6 faster than the original).
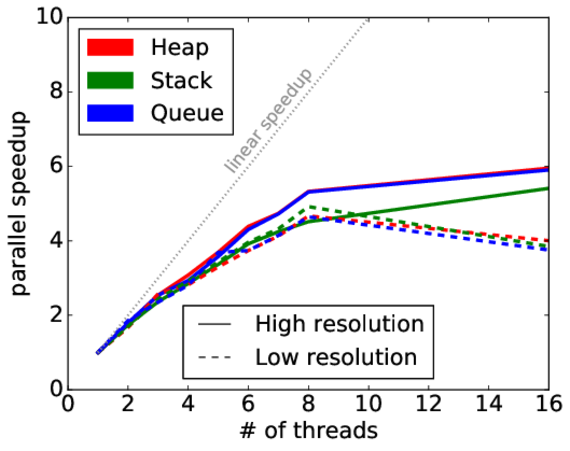
Fig. 3: Parallel speedup for the proposed parallel algorithm using a heap, stack and queue for the geometry shown in Fig. 1.



