 |
|
Biography
Karl Rupp was born in Austria in 1984. He received the BSc degree in electrical engineering from the Technische Universität Wien in 2006, the MSc in computational mathematics from Brunel University in 2007, and the degree of Diplomingenieur in microelectronics and in technical mathematics from the Technische Universität Wien in 2009. He completed his doctoral degree on deterministic numerical solutions of the Boltzmann transport equation in 2011. His scientific interests include discretization schemes and massively parallel algorithms in multiphysics problems.
Semiconductor Device Simulation on Next-Generation Hardware
Many different approaches to the simulation of semiconductors are in use today. At one end of the spectrum is the full quantum mechanical picture described by the Schrodinger equation, where individual charge carriers are modeled via wave functions. On the other, there are compact models that only describe a semiconductor device through a rather simple formula based on applied bias conditions. Within this spectrum of approaches, higher detail and accuracy demands higher computing power. The attractiveness of a particular approach therefore depends on the required level of detail and the available computing power. Thus, with more and more powerful computers, one may think it easy to simply crank up the simulation accuracy merely by switching to a more accurate semiconductor device simulation approach. Unfortunately, the full potential of modern hardware, and thus the benefit of higher accuracy, can only be leveraged if fine-grained parallelism of the hardware can be exposed within the simulation code.
With today's smartphones already offering processors with eight cores, the challenge is to use more than just a few compute cores for simulations on high-end computing hardware. To keep the possibly hundreds of computing units on modern parallel hardware busy, the simulation approach needs to be decomposed into many small subtasks with as few dependencies as possible. This requires a complete rethinking of established algorithms: The focus is no longer on tweaking a particular algorithm to extract a few percent of accuracy on a sequential processor, but rather to modify the approach such that it can be run on hundreds of computing units instead of only a single processor (cf. Fig. 1). As a consequence, approaches that parallelize well can make use of much higher computational power.
Our research is centered on the development of new parallel simulation approaches for semi-classical device simulation. This family of simulation approaches captures important quantum mechanical effects but is computationally much less expensive than a full quantum mechanical simulation. We revisit (and redesign) the algorithms used in semi-classical device simulation to run simulations on the latest processors with about 20 cores per socket, on graphics processing units and on field-programmable gate arrays.
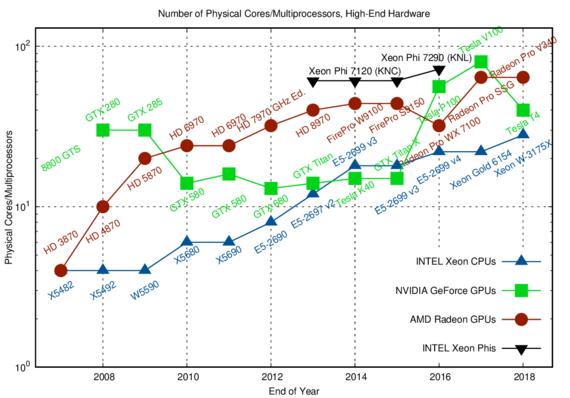
Fig. 1: The increase in parallelism (expressed by the number of processing cores) of high-end hardware over the last decade.



