Dominic Waldhör Dipl.-Ing. BSc Publications

The performance and lifetime of modern MOS transistors are severely affected by effects like Bias Temperature Instability (BTI) and Random Telegraph Noise (RTN). These reliability concerns are associated with single defects in the oxide or at the semiconductor/oxide interface that are able to trap charges from the conducting channel and thus cause a change in device electrostatics. Therefore, an accurate description of these charge transfer reactions is essential for the development of physically based reliability models.

BTI and RTN have recently been found to presumably have the same underlying cause and can therefore be described using a unified framework, namely the four-state nonradiative multiphonon (NMP) model. Within this model, oxide defects are assumed to have two positively charged states and two neutral states. Furthermore, by using the oft-applied Born-Oppenheimer approximation, the defect dynamics can be interpreted as movements along a potential energy surface (PES), which represents movement in a high-dimensional configuration space. In this picture, the stable defect states are given by the local minima of the PES. Charge transfer reactions between the substrate and the oxide defect are treated as a transition from one PES to another. According to the classical limit of quantum mechanical NMP theory, charge capture and emission events occur at the minimum energy crossing point (MECP) of two PESs. Usually, the challenge of finding the MECP in a high-dimensional configuration space can be avoided by treating the defect states as one-dimensional harmonic oscillators. The MECP is then assumed to be the intersection point of the respective parabolic energy profiles (see Fig. 1). This approach is commonly referred to as harmonic approximation. Although this approximation is very convenient and is widely used, its applicability to oxide defects has been assumed without rigorous justification so far.

In order to place NMP models on more solid ground, we investigated the accuracy of the crucial harmonic approximation using density functional theory (DFT). In our approach, DFT is coupled to a constrained optimization algorithm to locate the real MECP between two differently charged defect states. The transition barriers from the accurate but expensive MECP approach are used as a reference to evaluate the accuracy of the much simpler harmonic approximation. Our focus in this investigation is on prominent defects in amorphous SiO₂, i.e. oxygen vacancies, hydrogen bridges and hydroxyl-E’ centers (see Fig. 2). Our study clearly shows that the errors introduced by the harmonic approximation are small compared to the statistical spread of the transition barriers due to the amorphous structure of the host material (see Fig. 3). This interesting finding justifies the applicability of this approximation in reliability models used in modern TCAD software.

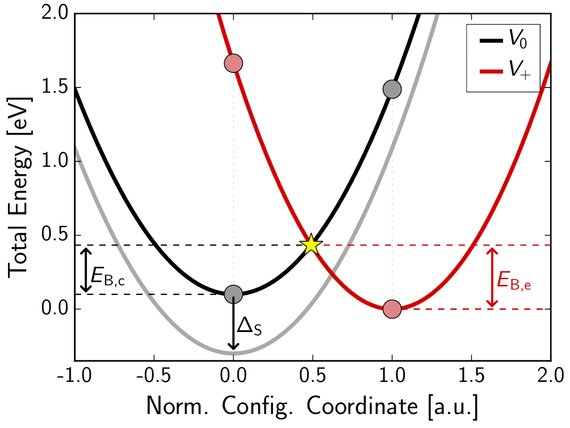
Fig. 1: PESs for different defect states can be approximated by parabolas. In the classical limit of NMP theory, the transition barriers are determined by the intersection point of the two PESs.

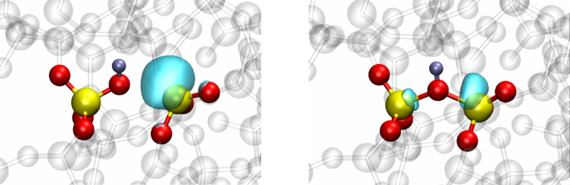
Fig. 2: The neutral (left) and positively charged (right) states of the hydroxyl-E’ center in amorphous SiO₂. The turquoise bubbles represent the HOMO and LUMO orbitals in the neutral and positive state, respectively.

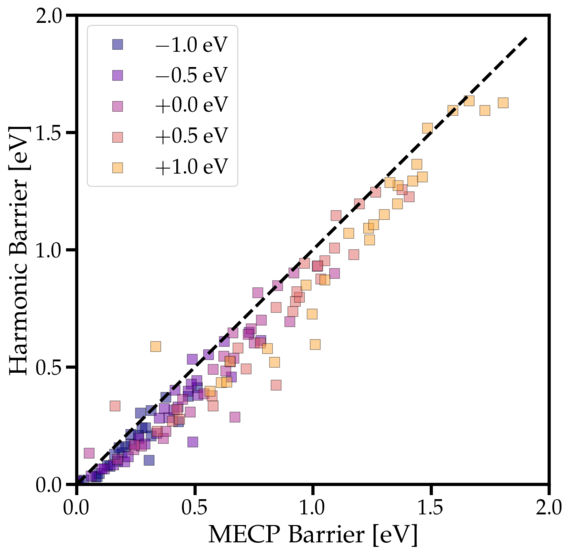
Fig. 3: Correlation between the resulting capture barriers for the harmonic approximation and the MECP approach for various applied biases. Although the harmonic approximation tends to slightly underestimate the barriers, it is in reasonable agreement with the exact barrier over the whole range of relevant biases.