The lattice scattering (acoustic phonons) and ionized impurity scattering, together with
piezoelectric scattering are the most relevant mechanisms which limit the mean free path of
carriers at low electric fields in SiC [124,125]. At low electric fields
the electron velocity increases almost linearly with the field. A widely used empirical
expression for the doping dependence of the low-field mobility is the Caughey-Thomas
equation [126].
 |
(3.77) |
where N
 and N
and N
 are the doping concentration of the dopants and
acceptors. The symbols
are the doping concentration of the dopants and
acceptors. The symbols
 ,
,
 , N
, N
 ,
,
 ,
,
 are fitting parameters. The parameter
are fitting parameters. The parameter
 denotes the mobility of undoped or unintentionally doped samples,
where lattice scattering is the main scattering mechanism, while
denotes the mobility of undoped or unintentionally doped samples,
where lattice scattering is the main scattering mechanism, while
 is the
mobility in highly doped material, where impurity scattering is dominant, given by
is the
mobility in highly doped material, where impurity scattering is dominant, given by
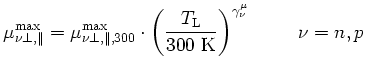 |
(3.78) |
 |
(3.79) |
 is the doping concentration at which the mobility is
(
is the doping concentration at which the mobility is
(
 /2,
/2,
 is a measure of how
quickly the mobility changes from
is a measure of how
quickly the mobility changes from
 to
to
 ,
,
 is a constant temperature coefficient, and
is a constant temperature coefficient, and
 specifies
how the undoped mobility changes due to lattice scattering. It is obvious from the previous
reasoning that the anisotropic mobility in
specifies
how the undoped mobility changes due to lattice scattering. It is obvious from the previous
reasoning that the anisotropic mobility in  -SiC is a tensor of second rank and has the
same form as the representative tensor
-SiC is a tensor of second rank and has the
same form as the representative tensor  in (3.2). However, a rigorous
modeling of the anisotropic properties of
in (3.2). However, a rigorous
modeling of the anisotropic properties of  -SiC is still a challenge to the
semiconductor transport theory.
-SiC is still a challenge to the
semiconductor transport theory.
A first attempt to calculate the anisotropy of the
Hall mobility in n-type  -SiC based on the band structure theory has been reported
in [127]. However, as the mobility parameters of semiconductors significantly
depend on the process technology, the reported mobility data from the period before wafers in
acceptable quality were available can hardly be used to investigate state-of-the-art
devices. Hall measurements of the bulk epitaxial free carrier mobility tensor components of
4H- and 6H-SiC have been reported [128,129]. The measured electron
mobility in 4H-SiC is about twice that of 6H-SiC for a total impurity concentration less than
-SiC based on the band structure theory has been reported
in [127]. However, as the mobility parameters of semiconductors significantly
depend on the process technology, the reported mobility data from the period before wafers in
acceptable quality were available can hardly be used to investigate state-of-the-art
devices. Hall measurements of the bulk epitaxial free carrier mobility tensor components of
4H- and 6H-SiC have been reported [128,129]. The measured electron
mobility in 4H-SiC is about twice that of 6H-SiC for a total impurity concentration less than
 cm
cm Additionally, the hole mobility in 4H-SiC is
Additionally, the hole mobility in 4H-SiC is  larger than in 6H-SiC
over the entire measured impurity range.
larger than in 6H-SiC
over the entire measured impurity range.
Figure 3.9:
The n-type (N) and p-type (Al)
mobility in  -SiC as a function of the doping concentration.
-SiC as a function of the doping concentration.
|
|
Schaffer et al. [128] investigated over  4H- and 6H-SiC wafers and
analyzed in detail the temperature dependence
4H- and 6H-SiC wafers and
analyzed in detail the temperature dependence  of both polytypes. They obtained
constant temperature coefficients
of both polytypes. They obtained
constant temperature coefficients
 for temperatures larger than 300 K in both
polytypes. Summary of the measured parameters for the low field mobility in 4H- and 6H-SiC are
listed in Table 3.5, and the corresponding model fitting is depicted in
Fig. 3.9.
for temperatures larger than 300 K in both
polytypes. Summary of the measured parameters for the low field mobility in 4H- and 6H-SiC are
listed in Table 3.5, and the corresponding model fitting is depicted in
Fig. 3.9.
The anisotropic characteristics of the Hall mobilities have
been investigated independently using epitaxial layers grown on [1100] and [1120]
surfaces. The results for N-doped (n-type) and Al-doped (p-type) 4H-SiC can be expressed as
 |
(3.80) |
 |
(3.81) |
similarly for 6H-SiC,
 |
(3.82) |
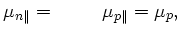 |
(3.83) |
for directions orthogonal ( ) and parallel (
) and parallel ( ) to the hexagonal c-axis. Thus,
the largest Hall mobility is related to a current flow parallel to the c-axis in 4H-SiC and
perpendicular to the c-axis in 6H-SiC. No dependence on the impurity concentration has been
reported for these ratios. On the other hand, a rather large dependence on temperature for
these ratios has been reported for both polytypes for
) to the hexagonal c-axis. Thus,
the largest Hall mobility is related to a current flow parallel to the c-axis in 4H-SiC and
perpendicular to the c-axis in 6H-SiC. No dependence on the impurity concentration has been
reported for these ratios. On the other hand, a rather large dependence on temperature for
these ratios has been reported for both polytypes for
 [128].
T. Ayalew: SiC Semiconductor Devices Technology, Modeling, and Simulation
[128].
T. Ayalew: SiC Semiconductor Devices Technology, Modeling, and Simulation
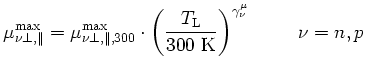

![]() is the doping concentration at which the mobility is
(
is the doping concentration at which the mobility is
(
![]() /2,
/2,
![]() is a measure of how
quickly the mobility changes from
is a measure of how
quickly the mobility changes from
![]() to
to
![]() ,
,
![]() is a constant temperature coefficient, and
is a constant temperature coefficient, and
![]() specifies
how the undoped mobility changes due to lattice scattering. It is obvious from the previous
reasoning that the anisotropic mobility in
specifies
how the undoped mobility changes due to lattice scattering. It is obvious from the previous
reasoning that the anisotropic mobility in ![]() -SiC is a tensor of second rank and has the
same form as the representative tensor
-SiC is a tensor of second rank and has the
same form as the representative tensor ![]() in (3.2). However, a rigorous
modeling of the anisotropic properties of
in (3.2). However, a rigorous
modeling of the anisotropic properties of ![]() -SiC is still a challenge to the
semiconductor transport theory.
-SiC is still a challenge to the
semiconductor transport theory.
![\includegraphics[width=0.6\linewidth]{figures/mobility.eps}](img424.png)