4.2.1 Semiconductor Hetero Interfaces
 
Two adjacent semiconductor segments are connected in the simulation by calculating the current J_n1 leaving segment 1 and J_n2 entering segment 2 as shown in  Figure 4.1. The current is described by the thermionic-field emission model with the equations [6]
 

(27)

 
and
 

.

(28)

 
The electron energy fluxes S_n1 and S_n2 across the heterojunction are given by
 

(29)

 
and
 

(30)

 
where
 

(31)

is the emission velocity. The height of the energy barrier for electrons between two semiconductors is
 

.

(32)

 
 

The function f(dE_C) which accounts for barrier lowering due to tunneling will be explained in the following. The profile of the energy barrier near the interface can be approximated by a triangular shape as shown in  Figure 4.1. The lowering of the effective barrier height dE_C due to tunneling through the energy barrier is modeled by
 

,

(33)

 
where  is the electric field perpendicular to the interface in segment 2 and x_eff is an effective tunnel length which is assumed to be 7 nm. The tunneling current through a potential barrier in first order is . Thus, the exponential function in (28) and (30) would read . To describe deviations from the idealized tunneling model the exponential function is expanded into a Tailor series. Therefore f(dE_C) in (28) and (30) becomes
 

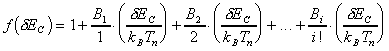(34)

 
where B_i have to be considered as fitting parameters for the simulation. Figure 4.2 illustrates a physical reason for the inadequacy of the idealized tunnel characteristics. It schematically shows the electron distribution in the channel of a delta doped DH­HEMT. The electrons in the whole simulation area are treated as classical particles, i. e. with zero spatial extension. This means that a simulated electron in the channel close to the interface experiences only the properties of the channel material. It is well known from quantum mechanics that the electron wave extends several nanometers which leads to non local effects such as quantization in a potential well as discussed in Section 2.2 [46].
 

The interface model given here describes a non local effect by a local relation. For instance the reduction in the energy barrier due to tunneling is determined by the electric field between the grid point right on the interface and the next grid point in the barrier perpendicular to the interface. Their separation is usually below 1 nm but the electron wave extends several nanometers into that layer as shown in  Figure 4.2. Therefore the actual energy barrier experienced by the electron cannot be predicted exactly. Based on the typical conduction band profile of HEMTs one expects that tunneling would be overestimated significantly if an exponential dependence on the electric field were used.
 

• 4.2.2 Semiconductor Passivation Interface
• 4.3 Physical Parameters
• 4.3.1 Effective Mass and Band Edge Energy
• 4.3.2 Mobility

   
Next: 4.2.2 Semiconductor Passivation Interface Up: 4.2 Interface Models Previous: 4.2 Interface Models