2.1 The Systems of Partial Differential Equations

The general form of the PDE systems describing the physical phenomena in process and interconnect technology can be expressed through the equation system,

$$\mathcal{L}(\mathbf{c})=\mathbf{f}(\mathbf{x})+\frac{\partial \mathbf{c}(\mathbf{x},t)}{\partial t},$$ (2.1)

which is defined on the simple bounded domain $\Omega\subset \Bbb{R}^3$. The PDE system (2.1) is fulfiled by functions $\mathbf{c}=(c_1,c_2,\dots,c_M)^T$, $c_i=c_i(\mathbf{x},t)\in \mathcal{V}_t=C^{2,1}(\Omega\times(0,\tau])$, for each $\tau\in \Bbb{R}^{+}$. We use the notation $\mathcal{L}(\mathbf{c})=(\mathcal{L}_1(\mathbf{c}),\dots,\mathcal{L}_M(\mathbf{c}))^T$, $\mathcal{L}_i$ is in our applications a second order nonlinear spatial differential operator and $\mathbf{f}=(f_1,f_2,\dots,f_M)^T$, $f_i(\mathbf{x})\in C(\Omega)$.

We assume that the domain $\Omega$ has a piecewise smooth boundary $\Gamma$. The general form of the boundary conditions applied on $\Gamma_i\in \Gamma (\forall i\neq j\Rightarrow \Gamma_i \cap\Gamma_j = \emptyset, \Gamma = \underset{i}{\bigcup}\; \Gamma_i)$,

$$\mathbf{A}_i\mathbf{c}+\mathbf{B}_i\frac{\partial\mathbf{c}}{\partial \mathbf{n}}=\mathbf{g}_i(\mathbf{c}), \Gamma_i,$$ (2.2)

where $\mathbf{A}_i$ and $\mathbf{B}_i$ are matrix consisting of functions sufficiently smooth on $\Gamma_i$ and $\mathbf{g}_i$ is a vector of continuous linear functionals. $\frac{\partial\mathbf{c}}{\partial \mathbf{n}}$ denotes the outward normal derivative. The problem also demands initial conditions for each unknown function $c_j(\mathbf{x},t)$,

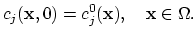$$c_j(\mathbf{x},0)=c_j^0(\mathbf{x}),\quad \mathbf{x}\in \Omega.$$ (2.3)

An approximate numerical solution is sought which in some way closely resembles the exact solution. Two methods of formulating such an approximate solution are: the Rayleigh-Ritz method and Galerkin's method. In order to express the main ideas more clearly we will explain these methods for the time invariant problems in the following two sections.