[prev] [prev-tail] [tail] [up]

2.3  Transformations

The material constants cij or sij for a particular material are usually specified in a basis with coordinate axes aligned with particular symmetry planes (if any) in the material. When solving problems involving anisotropic materials it is frequently necessary to transform these values to a coordinate system that is oriented in some convenient way relative to the boundaries of the solid. The basis transformation formulas are listed below and are used for the calculation of the dislocation energy in Chapter 3. To this end, let’s suppose that the components of the stiffness tensor are given in a basis, {e1,e2,e3}, and we wish to determine its components in a second basis, {m1,m2,m3}. We define the transformation tensor Ω with components Ωij = mj ⋅ ej, or in matrix form

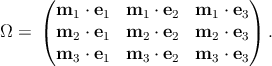( ) m1 ⋅ e1 m1 ⋅ e2 m1 ⋅ e3 Ω = ( m ⋅ e m ⋅ e m ⋅ e ) . 2 1 2 2 2 3 m3 ⋅ e1 m3 ⋅ e2 m3 ⋅ e3
(2.30)

This is a symmetric tensor satisfying ΩΩT = ΩTΩ = I. In practice, the transformation tensor can be computed in terms of the angles between the basis vectors. It is straightforward to show that stress, strain and elasticity tensors transform as

σij(m) = Ω ikσkl(e)Ω jl,
sij(m) = Ω ikσkl(e)σ jl,
cijkl(m) = Ω ipΩjqcpqrs(e)Ω krΩls. (2.31)
The basis transformation formula for the stiffness tensor C is more conveniently expressed in matrix form as
C(m) = KC(e)KT, (2.32)
where the rotation matrix K is computed as
K = ( ) K1 2K2 K3 K4, (2.33)
and
Kij1 = Ω ij2,
Kij2 = Ω imod(j+1,3)Ωimod(j+2,3),
Kij3 = Ω mod(i+1,3)jΩmod(i+2,3)j,
Kij4 = Ω mod(i+1,3)mod(j+1,3)Ωmod(j+2,3)mod(j+2,3)+
Ωmod(i+1,3)mod(j+2,3)Ωmod(i+2,3)mod(j+1,3),
with i,j = 1, 2, 3. (2.34)
The modulo function satisfies
{ ii ≤ 3 mod (i,3) = i - 3i > 3 .
(2.35)

The basis change for the compliance tensor (the inverse of the stiffness tensor) follows as

S(m) = K-TS(e)K-1, (2.36)
where
K-T = ( 1 2) K 3 K 4 2K K. (2.37)
The proof of these expressions is given in Ting  [74]. For the particular case of rotation around an angle θ in a counterclockwise sense about the x,y,z axes, the rotation matrix reduces, respectively, to
( 1 0 0 0 0 0 ) | 2 2 | | 0 c2 s2 2cs 0 0 | || 0 s c - 2cs 0 0 || || 0 - cs cs c2 - s2 0 0 || ( 0 0 0 0 c - s) 0 0 0 0 - s c( c2 0 s2 0 2cs 0 ) | | | 02 1 02 0 0 0 | || s 0 c 0 - 2cs 0 || || 0 0 0 c 0 - s|| ( - cs 0 cs 0 c2 - s2 0 ) 0 0 0 s 0 c( c2 s2 0 0 0 2cs ) | 2 2 | | s c 0 0 0 - 2cs | || 0 0 1 0 0 0 || || 0 0 0 c s 0 || ( 0 0 0 - s c 0 ) - cs cs 0 0 0 c2 - s2,
(2.38)
where c = cos θ and s = sin θ. The inverse matrix K-1 can be obtained simply by changing the sign of the angle θ in each rotation matrix. Clearly, applying the three rotations successively can produce an arbitrary orientation change.

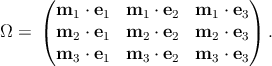
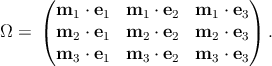
[prev] [prev-tail] [front] [up]