



Next: 4.5 Inversion Layer Mobility
Up: 4. Mobility Modeling
Previous: 4.3 Bulk Mobility of
4.4 Bulk Mobility of Strained Ge
The model equations derived in Section 4.3.2 for calculating the
mobility in strained Si can also be applied to estimate the mobility in
strained Ge. This could be very useful since recently the possibility of
utilizing Ge as a channel material [Liu05] [Low04] [Yeo05]
is being explored for the next generation CMOS technologies. This interest
stems from the significantly higher carrier mobilities in Ge in comparison to
Si.
In Ge the conduction band minima consist of four degenerate pairs of
 -valleys located along the
-valleys located along the
 directions. Application of
strain lifts the degeneracy of the valleys. The valley splitting for the
directions. Application of
strain lifts the degeneracy of the valleys. The valley splitting for the
 valley-pair can be calculated using (3.42) and the mobility
tensor can be expressed as
valley-pair can be calculated using (3.42) and the mobility
tensor can be expressed as
![$\displaystyle \ensuremath{{\underline{\mu}}}_{\ensuremath{{\mathrm{n}}}}^{\text...
...*{1cm} \normalsize i = [111],[\overline{1}11],[11\overline{1}],[1\overline{1}1]$](img613.png) |
(4.83) |
Here the scaled inverse mass tensors given by
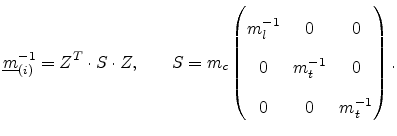 |
(4.84) |
The masses are
 and
and
 and the
transformation matrices are given as,
and the
transformation matrices are given as,
For uniaxial compressive strain along the ![$ [111]$](img209.png) direction, the valley pairs
located along the
direction, the valley pairs
located along the ![$ [111]$](img209.png) direction (
direction ( ) are lowered in energy, while the
remaining three valley pairs (
) are lowered in energy, while the
remaining three valley pairs ( ,
,  ,
,  ) move up in energy and remain
degenerate.
By this effect, the transport mass in the (111) plane is lowered and
inter-valley phonon scattering is reduced, which results in a mobility
enhancement.
) move up in energy and remain
degenerate.
By this effect, the transport mass in the (111) plane is lowered and
inter-valley phonon scattering is reduced, which results in a mobility
enhancement.
The temperature dependence of the mobility for the strained case can be fit
using a power law expression.
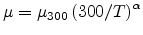 |
(4.87) |
Here  is the bulk mobility at 300K and
is the bulk mobility at 300K and  is a parameter. The
temperature dependence is introduced into the analytical model through the
enhancement factor
is a parameter. The
temperature dependence is introduced into the analytical model through the
enhancement factor  as
as
 |
(4.88) |
where  is the mobility enhancement in unstrained Ge at 300K. The
lattice temperature also affects the mobility through the inter-valley
scattering rate (4.61) and the valley
populations (4.39).
is the mobility enhancement in unstrained Ge at 300K. The
lattice temperature also affects the mobility through the inter-valley
scattering rate (4.61) and the valley
populations (4.39).




Next: 4.5 Inversion Layer Mobility
Up: 4. Mobility Modeling
Previous: 4.3 Bulk Mobility of
S. Dhar: Analytical Mobility Modeling for Strained Silicon-Based Devices
![]() -valleys located along the
-valleys located along the
![]() directions. Application of
strain lifts the degeneracy of the valleys. The valley splitting for the
directions. Application of
strain lifts the degeneracy of the valleys. The valley splitting for the
![]() valley-pair can be calculated using (3.42) and the mobility
tensor can be expressed as
valley-pair can be calculated using (3.42) and the mobility
tensor can be expressed as
![$\displaystyle \ensuremath{{\underline{\mu}}}_{\ensuremath{{\mathrm{n}}}}^{\text...
...*{1cm} \normalsize i = [111],[\overline{1}11],[11\overline{1}],[1\overline{1}1]$](img613.png)
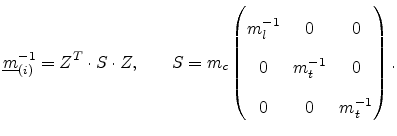
![$\displaystyle Z_{[111]} = \begin{pmatrix}\frac{1}{\sqrt{3}} & \! \frac{1}{\sqrt...
...\sqrt{6}} & \! \frac{-1}{\sqrt{6}} & \! \frac{\sqrt{2}}{\sqrt{3}} \end{pmatrix}$](img617.png)
![$\displaystyle Z_{[11\overline{1}]} = \begin{pmatrix}\frac{-1}{\sqrt{3}} & \! \f...
...{\sqrt{6}} & \! \frac{1}{\sqrt{6}} & \! \frac{\sqrt{2}}{\sqrt{3}} \end{pmatrix}$](img618.png)
![]() direction, the valley pairs
located along the
direction, the valley pairs
located along the ![]() direction (
direction (![]() ) are lowered in energy, while the
remaining three valley pairs (
) are lowered in energy, while the
remaining three valley pairs (![]() ,
, ![]() ,
, ![]() ) move up in energy and remain
degenerate.
By this effect, the transport mass in the (111) plane is lowered and
inter-valley phonon scattering is reduced, which results in a mobility
enhancement.
) move up in energy and remain
degenerate.
By this effect, the transport mass in the (111) plane is lowered and
inter-valley phonon scattering is reduced, which results in a mobility
enhancement.