3.2.3 Stability

In time integration schemes, such as the first-order forward Euler method, information from a grid point to a neighbor grid point can at most propagate with the velocity given by the ratio of the grid spacing and the time increment, $\frac{{\Delta x}}{\Delta{t}}$ . In order to calculate the movement of a surface, its maximum speed must be smaller than this critical value

$$\max_{{\vec{p}}\in{\mathcal{G}}} \left\vert{V}({\vec{p}})\right\vert \leq \frac{{\Delta x}}{\Delta{t}}.$$ (3.15)

This condition needs to be fulfilled in order to guarantee a stable time integration and is known as the Courant-Friedrichs-Lewy (CFL) condition [24].

For each integration step the time increment must be adapted to fulfill the CFL condition. In practice, a positive constant ${C_\text{CFL}}\in\left]0,1\right]$ , the so-called CFL number, is defined and an appropriate time increment is chosen according to

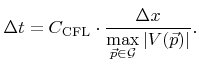$$\Delta{t}={C_\text{CFL}}\cdot\frac{{\Delta x}}{{\displaystyle\max_{{\vec{p}}\in{\mathcal{G}}} \left\vert{V}({\vec{p}})\right\vert}}.$$ (3.16)