2.4.3.4 Non-Equilibrium GREEN's Function Device Simulation

The non-equilibrium GREEN's function formalism (NEGF) provides a powerful means to handle open quantum systems. These are systems which are not confined but connected to reservoirs and have non-vanishing boundary conditions for the wave functions in SCHRÖDINGER's equation (2.13). The HAMILTONian of such a reservoir-coupled device can be written as

$$\left( \begin{array}{cc} \ensuremath{{\underline{H}}}& \ensuremat... ...emath{{\underline{C}}}^+ & \ensuremath{{\underline{H}}}_R \end{array}\right)\ ,$$

where $\ensuremath{{\underline{H}}}$ and $\ensuremath{{\underline{H}}}_R$ denote the HAMILTONian of the device and the reservoir and $\ensuremath{{\underline{C}}}$ represents a coupling matrix. In real systems, the dimension of $\ensuremath{{\underline{H}}}_R$ is usually much larger than the dimension of $\ensuremath{{\underline{H}}}$. Note that $\ensuremath{{\underline{H}}}$ is not HERMITian^2.12, like in a closed system, and it therefore admits complex eigenvalues. The corresponding single-particle GREEN's function reads

$$\left( \begin{array}{cc} \ensuremath{{\underline{G}}}& \ensuremat... ...{\underline{I}}}+ \ensuremath{{\underline{H}}}_R \\ \end{array} \right)^{-1}\ ,$$ (2.24)

where $\ensuremath{{\underline{G}}}_{DR}$ and $\ensuremath{{\underline{G}}}_{RD}$ refer to the coupling of the device to the reservoir, and $\ensuremath{{\underline{G}}}_{R}$ describes the reservoir itself. It can be shown that $\ensuremath{{\underline{G}}}$, the retarded GREEN's function, becomes

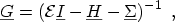$$\ensuremath{{\underline{G}}}= \left( {\mathcal{E}}\ensuremath{{\u... ... \ensuremath{{\underline{H}}}- \ensuremath{{\underline{\Sigma}}}\right)^{-1}\ ,$$ (2.25)

where $\ensuremath{{\underline{\Sigma}}}$ denotes the self energy matrix which describes the interaction of the reservoir with the device [92,93,94,95]. This has the advantage that the reservoir, which may be of much larger dimensions than the device, only enters the problem via the self energy matrix which has the same dimension as the device HAMILTONian. From the retarded GREEN's function, the spectral function $\ensuremath{{\underline{A}}}$ can be derived

$$\ensuremath{{\underline{A}}}({\mathcal{E}}) = \imath(\ensuremath{... ...derline{G}}}({\mathcal{E}}) - \ensuremath{{\underline{G}}}^+({\mathcal{E}}))\ ,$$ (2.26)

from which the carrier concentration in the device is calculated by

$$\ensuremath{{\underline{D}}}= \frac{m{\mathrm{k_B}}T}{2\pi^2\hbar... ...}}}{{\mathrm{k_B}}T}\right) \right) \, \ensuremath {\mathrm{d}}{\mathcal{E}}\ .$$ (2.27)

A. Gehring: Simulation of Tunneling in Semiconductor Devices