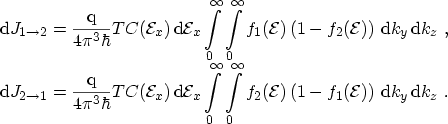3.2 The TSU-ESAKI Model

The processes ECB and HVB shown in Fig. 3.1 can be investigated considering an energy barrier as shown in Fig. 3.2. Two semiconductor or metal regions are separated by an energy barrier with barrier height $\ensuremath {\mathrm{q}}\ensuremath{\Phi_\mathrm{B}}$, measured from the FERMI energy to the conduction band edge of the insulating layer. Electrons tunnel from Electrode 1 to Electrode 2. The distribution functions at both sides of the barrier are indicated in the figure.

Figure 3.2: Energy barrier with two electrodes which can be used to describe the ECB or HVB processes.

In the following derivation some assumptions will be made which are necessary to allow an easy incorporation of the model in a device simulator. These are:

• Effective-mass approximation: The different masses corresponding to the band structure of the considered material are lumped into a single value for the effective mass. This is denoted by $m_\mathrm{eff}$ in the electrodes and $m_\mathrm{diel}$ in the dielectric layer.
• Parabolic bands: The dispersion relation in semiconductors is approximated by

  $${\mathcal{E}}= \frac{\hbar^2 {\mathbf{k}}^2}{2\ensuremath{m_\math... ...f}}} = \frac{\hbar^2 (k_x^2 + k_y^2 + k_z^2)}{2\ensuremath{m_\mathrm{eff}}} \ ,$$ (3.1)

  
  
  with the wave vector $\mathbf{k} = k_x {\mathbf{e_x}} + k_y{\mathbf{e_y}} + k_z{\mathbf{e_z}}$.
• Conservation of parallel momentum: Only transitions in the $x$-direction are considered, the parallel wave vector ${\mathbf{k_\rho}} = (k_y{\mathbf{e_y}} + k_z{\mathbf{e_z}})$ is not altered by the tunneling process.

The net tunneling current density from Electrode 1 to Electrode 2 can be written as the net difference between current flowing from Side 1 to Side 2 and vice versa [96,97]

$$J=J_{1\to 2} - J_{2\to 1}\ .$$ (3.2)

The current density through the two interfaces depends on the perpendicular component of the wave vector $k_x$, the transmission coefficient $TC$, the perpendicular velocity $v_x$, the density of states $g$, and the distribution function at both sides of the barrier:

$$\begin{array}{l} \ensuremath {\mathrm{d}}J_{1\to 2} = \ensure... ...({\mathcal{E}})) \, \ensuremath {\mathrm{d}}k_x \ . \end{array}$$ (3.3)

In this expression it is assumed that the transmission coefficient only depends on the momentum perpendicular to the interface. The density of $k_x$ states $g(k_x)$ is

$$g(k_x) = \int_0^\infty \int_0^\infty g(k_x, k_y, k_z) \,\ensuremath {\mathrm{d}}k_y \,\ensuremath {\mathrm{d}}k_z \ ,$$ (3.4)

where $g(k_x,k_y,k_z)$ denotes the three-dimensional density of states in the momentum space. Considering the quantized wave vector components within a cube of side length $L$

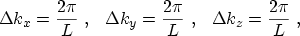$$\begin{array}{lll} \Delta k_x = \displaystyle \frac{2\pi}{L}\... ...\ , & \Delta k_z = \displaystyle \frac{2\pi}{L} \ , \end{array}$$ (3.5)

yields for the density of states within the cube

$$g(k_x,k_y,k_z) = 2 \frac{1}{\Delta k_x \Delta k_y \Delta k_z} \frac{1}{L^3} = \frac{1}{4\pi^3} \ ,$$ (3.6)

where the factor 2 stems from spin degeneracy. For the parabolic dispersion relation (3.1) the velocity and energy components in tunneling direction obey

$$\begin{array}{lll} \displaystyle v_x = \frac{1}{\hbar}\frac{\... ...{\hbar} \ensuremath {\mathrm{d}}{\mathcal{E}}_x \ . \end{array}$$ (3.7)

Hence, expressions (3.3) become

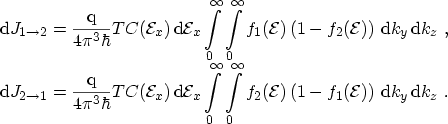$$\begin{array}{l} \ensuremath {\mathrm{d}}J_{1\to 2} = \displa... ...h {\mathrm{d}}k_y \,\ensuremath {\mathrm{d}}k_z \ . \end{array}$$ (3.8)

Using polar coordinates for the parallel wave vector components

$$\begin{array}{ll} \displaystyle k_\rho = \sqrt{k_y^2 + k_z^2}... ...ht)\ , & k_z = k_\rho \sin\left( \gamma \right) \ , \end{array}$$ (3.9)

the current density evaluates to

$$\begin{array}{l} \displaystyle J_{1\to 2} = \frac{4\pi \ensur... ...ht)\,\ensuremath {\mathrm{d}}{\mathcal{E}}_\rho \ . \end{array}$$ (3.10)

In these expressions the total energy ${\mathcal{E}}$ has been split into a longitudinal part ${\mathcal{E}}_\rho$ and a transversal part ${\mathcal{E}}_x$

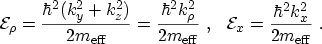$$\begin{array}{ll} \displaystyle {\mathcal{E}}_\rho = \frac{\h... ...rac{\hbar^2k_x^2}{2\ensuremath{m_\mathrm{eff}}} \ . \end{array}$$ (3.11)

Evaluating the difference $J = J_{1\to 2} - J_{2\to 1}$, the net current through the interface equals

$$J=\frac{4 \pi \ensuremath{m_\mathrm{eff}}\ensuremath {\mathrm{q}}... ...}) -f_2({\mathcal{E}})\right) \, \ensuremath {\mathrm{d}}{\mathcal{E}}_\rho \ .$$ (3.12)

This expression is usually written as an integral over the product of two independent parts which only depend on the energy perpendicular to the interface: the transmission coefficient $TC({\mathcal{E}}_x)$ and the supply function $N({\mathcal{E}}_x)$:

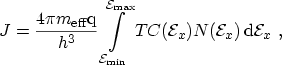$$J = \frac{4\pi \ensuremath{m_\mathrm{eff}}\ensuremath {\mathrm{q}... ...\mathcal{E}}_x) N({\mathcal{E}}_x)\,\ensuremath {\mathrm{d}}{\mathcal{E}}_x \ ,$$ (3.13)

which is the expression known as TSU-ESAKI formula. This model has been proposed by DUKE [98] and was used by TSU and ESAKI for the modeling of tunneling current in resonant tunneling devices [99]. The values of $\ensuremath{{\mathcal{E}}_\mathrm{min}}$ and $\ensuremath{{\mathcal{E}}_\mathrm{max}}$ depend on the considered tunneling process:

• Electrons tunneling from the conduction band (ECB): $\ensuremath{{\mathcal{E}}_\mathrm{min}}$ is the highest conduction band edge of the two electrodes, $\ensuremath{{\mathcal{E}}_\mathrm{max}}$ is the highest conduction band edge of the dielectric.
• Holes tunneling from the valence band (HVB): $\ensuremath{{\mathcal{E}}_\mathrm{min}}$ is the absolute value of the lowest valence band edge of the electrodes, $\ensuremath{{\mathcal{E}}_\mathrm{max}}$ is the absolute value of the lowest valence band edge of the dielectric. The sign of the integration must be changed.
• Electrons tunneling from the valence band (EVB): $\ensuremath{{\mathcal{E}}_\mathrm{min}}$ is the lowest conduction band edge of the two electrodes, $\ensuremath{{\mathcal{E}}_\mathrm{max}}$ the highest valence band edge of the two electrodes. It must be checked if $\ensuremath{{\mathcal{E}}_\mathrm{min}}<\ensuremath{{\mathcal{E}}_\mathrm{max}}$.

The next sections concentrate on the calculation of the supply function and the transmission coefficient.

A. Gehring: Simulation of Tunneling in Semiconductor Devices