3.6.3 The Life Time of Quasi-Bound States

The tunneling current from quasi-bound states in (3.92) depends on their quantum-mechanical life time $\ensuremath{\tau_{\mathrm{q}}}$: In contrast to electrons in bound states, which have an infinite life time, electrons in quasi-bound states have a non-zero probability to tunnel through the energy barrier, thus their life time is finite [165,166,167]. This can be seen if the time time evolution of the states is considered [168]

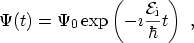$$\Psi(t) = \Psi_0 \exp\left( -\imath\frac{\ensuremath{{\mathcal{E}}_\mathrm{i}}}{\hbar}t\right) \ ,$$ (3.104)

where $\Psi_0$ is the initial wave function and the complex eigenenergy is

$$\ensuremath{{\mathcal{E}}_\mathrm{i}}= \ensuremath {{\mathcal{E}}_\mathrm{re}}- \imath \ensuremath {{\mathcal{E}}_\mathrm{im}}\ .$$ (3.105)

The time-dependent probability becomes

$$P(t) = \Psi^\ast(t) \Psi(t) = \Psi_0 ^2 \exp \left( -\frac{2\ensu... ...t) = \Psi_0 ^2 \exp \left( -\frac{t}{\ensuremath{\tau_{\mathrm{q}}}} \right)\ .$$ (3.106)

Thus, the imaginary component of the eigenenergy ${\mathcal{E}}$ is related to the decay time constant by

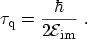$$\ensuremath{\tau_{\mathrm{q}}}= \frac{\hbar}{2 \ensuremath {{\mathcal{E}}_\mathrm{im}}} \ .$$ (3.107)

The QBS are frequently used for tunneling current calculations [169,170,171,172,173,174]. Three methods are established to compute the life time of a quasi-bound state in MOS inversion layers: Computing the full-width half-maximum (FWHM) of the reflection coefficient resonances, using the quasi-classical formula based on the WENTZEL-KRAMERS-BRILLOUIN-method, or from the complex eigenvalues of the non-HERMITian HAMILTONian. These methods will be described in the following.

Subsections

• 3.6.3.1 The Reflection Coefficient Resonances
• 3.6.3.2 The Quasi-Classical Formula
• 3.6.3.3 The Eigenvalues of the Non-HERMITian HAMILTONian

A. Gehring: Simulation of Tunneling in Semiconductor Devices