3.6.3.1 The Reflection Coefficient Resonances

A quasi-bound state forms if one of the system boundary conditions is open ($\neq 0$) and the other one is closed ($=0$). The carrier wave function is reflected at the interface, there is no transmitted wave. Using the transfer-matrix method described in Section 3.5.3, the system can be described by

$$\left( \begin{array}{c} \ensuremath{A_\mathrm{N}}\\ \ensuremath{B... ...array} \right) \left( \begin{array}{c} A_{1} \\ B_{1} \\ \end{array} \right)\ ,$$ (3.108)

where the wave functions are plane waves

$$\Psi_j(x) = A_j \exp(\imath k_j x) + B_j\exp(-\imath k_j x) \ .$$ (3.109)

However, no transmission coefficient can be defined for a quasi-bound state: The transmitted wave amplitude $\ensuremath{A_\mathrm{N}}$ must vanish to fulfill the assumption of closed boundary conditions. Instead, a reflection coefficient can be defined which is

$$RC({\mathcal{E}}) = \frac{B_1}{A_1} = -\frac{T_{21}}{T_{22}} \ .$$ (3.110)

It is shown in [165] that for a quasi-bound state, the transfer matrix is not HERMITian^3.9 and its elements obey

$$T_{11} = T_{12}^\ast\ ,$$

$$T_{21} = T_{22}^\ast\ .$$

Therefore, the reflection coefficient $RC({\mathcal{E}})$ can be written as

$$RC({\mathcal{E}}) = \exp\left(\imath\Theta({\mathcal{E}})\right) \ .$$ (3.111)

The phase $\Theta({\mathcal{E}})$ varies only weakly at energies away from the resonance energy of the QBS, while near the QBS the phase changes strongly. Near the complex energy levels $\ensuremath{{\mathcal{E}}_\mathrm{i}}$ the derivative of the phase factor $\Theta({\mathcal{E}})$ follows a LORENTZian^3.10 distribution

$$\frac{\ensuremath {\mathrm{d}}\Theta}{\ensuremath {\mathrm{d}}{\m... ...\mathrm{re}})^2 + \displaystyle \ensuremath {{\mathcal{E}}_\mathrm{im}}^2 } \ ,$$ (3.112)

where $2\ensuremath {{\mathcal{E}}_\mathrm{im}}$ is the full-width half-maximum (FWHM) value of $\ensuremath {\mathrm{d}}\Theta/\ensuremath {\mathrm{d}}{\mathcal{E}}$. Thus, by calculating the phase of the reflection coefficient as a function of energy, the life times can be determined. This method has been studied intensely by CASSAN et al. [160,175]. They reported numerical difficulties in the calculation of the value of $\ensuremath {\mathrm{d}}\Theta/\ensuremath {\mathrm{d}}{\mathcal{E}}$ which is prone to numerical noise. Similar problems have been reported by other groups [176].

An alternative approach has been presented by CLERC et al. who noted that the life times can also be extracted directly from the transfer matrix [144]. For a free state, $\ensuremath{B_\mathrm{N}}=0$ in (3.108) and the transmission coefficient becomes

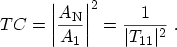$$TC = \left\vert\frac{\ensuremath{A_\mathrm{N}}}{A_1}\right\vert^2 = \frac{1}{\vert T_{11}\vert^2}\ .$$ (3.113)

For a quasi-bound state, $\ensuremath{A_\mathrm{N}}=0$. Therefore,

$$A_1 = T_{12} \ensuremath{B_\mathrm{N}}\ ,$$ (3.114)

but, since $T_{11} = T_{12}^*$, the value of $\vert T_{11}\vert^{-2}$ may be evaluated as well -- even if it cannot be interpreted as a transmission coefficient. The life time of the QBS is again found from the resonance peak of the LORENTZian around the real component of the eigenenergy $\ensuremath {{\mathcal{E}}_\mathrm{re}}$

$$\frac{1}{\vert T_{11}\vert^2} = \frac{1}{({\mathcal{E}}- \ensurem... ...{re}})^2 + \displaystyle \frac{\hbar^2}{4\ensuremath{\tau_{\mathrm{q}}}^2}} \ ,$$ (3.115)

but no derivative must be calculated this time. As an example of this method the left part of Fig. 3.14 shows the shape of the conduction band edge of a MOS structure in the substrate, dielectric, and polysilicon gate. In the substrate a triangular quantum well forms. Considering closed boundaries, eigenvalues and wave functions can be calculated. The corresponding wave functions are shown in the figure, where closed boundary conditions have been used at the boundaries of the simulation domain. Note the wave function penetration into the classically forbidden region of the dielectric layer. The eigenvalues of the quasi-bound states are located at 0.27, 0.47, 0.63, 0.76, 0.86, and 0.95eV. The same information can be found when the value of $\vert T_{11}\vert^{-2}$ is investigated, as shown in right part of Fig. 3.14: Every quasi-bound state in the inversion layer manifests as a peak in the value of $\vert T_{11}\vert^{-2}$. The width of each peak is directly related to its life time.

Figure 3.14: Wave function of quasi-bound states. Note the wave function penetration into classically forbidden regions (left). The respective value of $\vert T_{11}\vert^{-2}$ as a function of energy is shown in the right plot. The energy broadening around the poles is clearly visible.

A. Gehring: Simulation of Tunneling in Semiconductor Devices