3.8.1.3 Compact Trap-Assisted Tunneling Models

For application in circuit simulators, or to catch a quick glimpse at the effects of trap-assisted tunneling, compact models are required. A frequently used expression is based on the work of RICCO et al. [193]. They describe the trapping- and detrapping processes by

$$\ensuremath{J_\mathrm{TAT}}= J \ensuremath{C_\mathrm{T}}TC_1 (\en... ...{n_\mathrm{T}}) = \ensuremath {\mathrm{q}}\nu \ensuremath{n_\mathrm{T}}TC_2 \ ,$$ (3.126)

where $J$ is the supply current density at the interface, $\ensuremath{C_\mathrm{T}}$ the capture cross section, $TC_1$ and $TC_2$ the transmission coefficients from the left and right side of the dielectric to the trap, $\ensuremath{n_\mathrm{T}}$ the concentration of trapped electrons which is smaller or equal than the trap concentration $\ensuremath{N_\mathrm{T}}$, and $\nu$ their escape frequency. The highest contribution comes from traps which have $TC_1 \approx TC_2$, therefore the trap-assisted tunnel current becomes

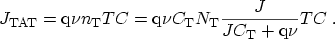$$\ensuremath{J_\mathrm{TAT}}= \ensuremath {\mathrm{q}}\nu \ensurem... ...rm{T}}\frac{J}{J \ensuremath{C_\mathrm{T}}+ \ensuremath {\mathrm{q}}\nu} TC \ .$$ (3.127)

A modified version of this expression was used by GHETTI et al. [195,211]. Other more or less empirical trap-assisted tunneling models based on SILC measurements are presented in [212]. These comprise hopping conduction

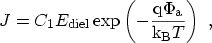$$J = C_1 \ensuremath{E_\mathrm{diel}}\exp\left( -\frac{\ensuremath {\mathrm{q}}\ensuremath{\Phi_\mathrm{a}}}{{\mathrm{k_B}}T} \right)\ ,$$ (3.128)

where $\ensuremath{\Phi_\mathrm{a}}$ is an activation potential, and the frequently applied POOLE-FRENKEL tunneling formula [213,214,215,212,216,217,218]. This model describes the emission of trapped electrons and reads

$$J = A \ensuremath{E_\mathrm{diel}}\exp\left( -\frac{\ensuremath{{... ...remath {\mathrm{q}}\ensuremath{E_\mathrm{diel}}}{\pi \kappa_0 r^2}} \right) \ ,$$ (3.129)

where $r$ is the refractive index of the dielectric, $\ensuremath{{\mathcal{E}}_\mathrm{T}}$ is the difference between the conduction band in the dielectric and the trap energy, and the coefficient $A$ depends on the trap concentration. The main motivation to use this expression is that the trap-assisted gate current density was found to be a linear function of the square root of the dielectric field, in contrast to the FOWLER-NORDHEIM tunneling current which is a linear function of the dielectric field. Note, however, that no trapping-detrapping considerations enter this equation.

A. Gehring: Simulation of Tunneling in Semiconductor Devices