2.3.3.3 Linear Capacitor

The constitutive relation for a linear capacitor is I = C ^. dV/dt. For the backward Euler discretization scheme the equations are as follows

$$\left(\vphantom{V - V_o}\right. \left.\vphantom{V - V_o}\right)$$ I = (2.35)

$${\frac{C}{\Delta t}}$$ G = (2.36)

The stamp is given as

yx, y	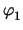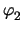$\varphi_{1}^{}$	$\varphi_{2}^{}$	f
n1	G	- G	- I
n2	- G	G	I

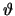For thermal capacitors C is substituted by C_th and $\varphi$ by $\vartheta$, respectively.